三角比とは？sin(正弦), cos(余弦), tan(正接) の定義と覚え方！

三角定規の直角三角形の辺の比（1 : 2 : √3、1 : 1 : √2）は中学までで学びましたね。ここでは、それをもっと一般化させていきましょう。

実は、どんな直角三角形であっても、その辺の「比」は、直角でない1つの角の大きさによって完全に決まります。例えば、こんなイメージです。

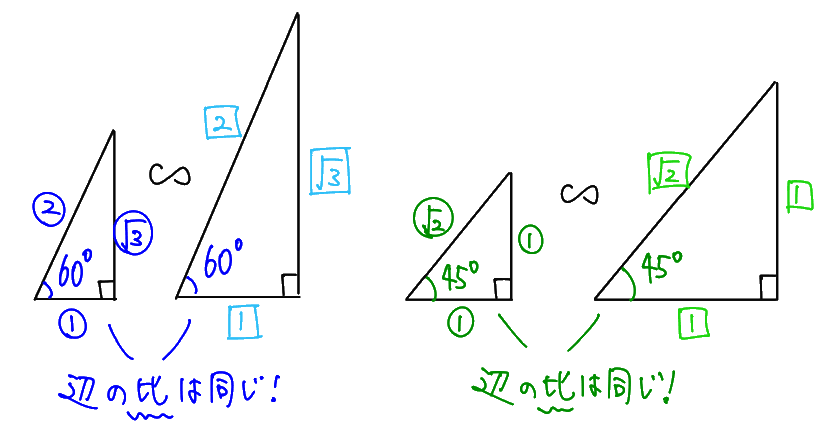
これは、直角でない1つの角の大きさが同じ直角三角形同士は、全ての角が等しくなるので、相似になるからです。相似な図形であれば、辺の長さが変わっても、その「比」は同じになることを思い出しましょう。

それならば、直角三角形を考えて、（直角でない）1つの角の大きさによって、直角三角形の辺の比を表そうというのが、「三角比」で最初にやりたいことになります。（直角「三角」形の辺の「比」というイメージです！）

そこで、辺の比を分数で表すことにして、下の3つを考えます。

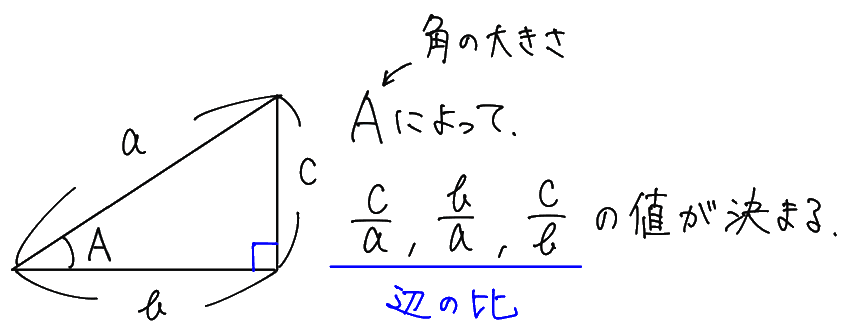
これらの値は、角の大きさAだけによって1つに決まることに注意して、これらを sin A, cos A, tan A と名付けます。

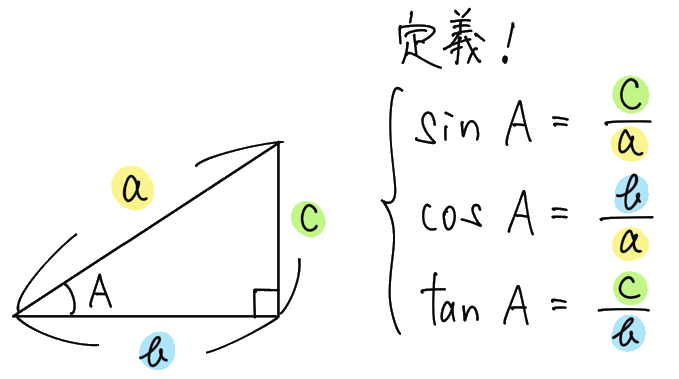
これで三角比が定義できました！

• sin A の値を A のサイン（正弦）

• cos A の値を A のコサイン（余弦）

• tan A の値を A のタンジェント（正接）

と呼びます。

覚え方としては、こんな感じで、それぞれの頭文字「s, c, t」を筆記体で書いて、三角形の辺をなぞっていき、分母→分子の順に並べるものが有名です。

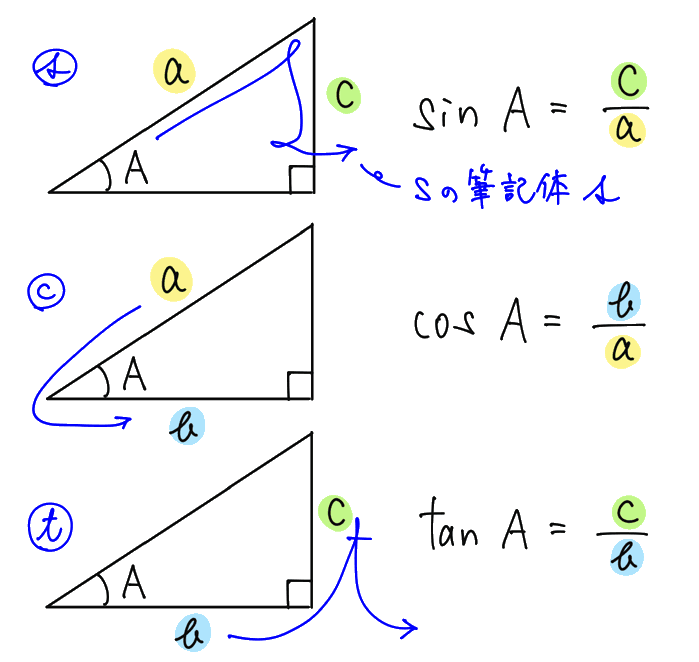
とりあえず、これは定義なので覚える必要があります。覚え方はなんでもいいので、確実に覚えましょう！

三角比の基本

では、おなじみの三角定規の直角三角形で、三角比を求めてみましょう。辺の比を求めていけばOKです。

30°, 45°, 60°の三角比

まずは、下の30°-60°-90°の直角三角形を考えてみましょう。∠A に注目すると、それぞれの辺の比から30°の三角比が求められます。

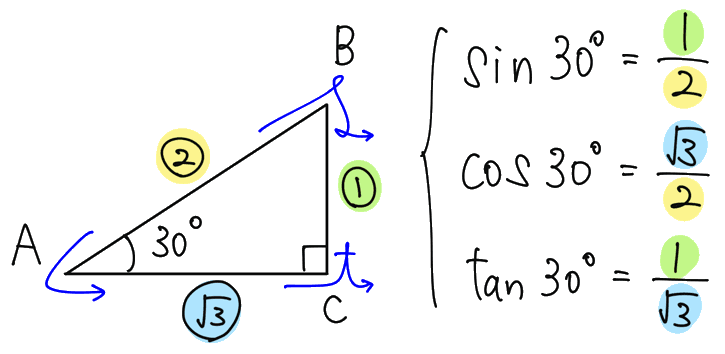
また、向きを変えたこちらの30°-60°-90°の直角三角形を考えて、∠A に注目すると、このように60°の三角比が求められます。

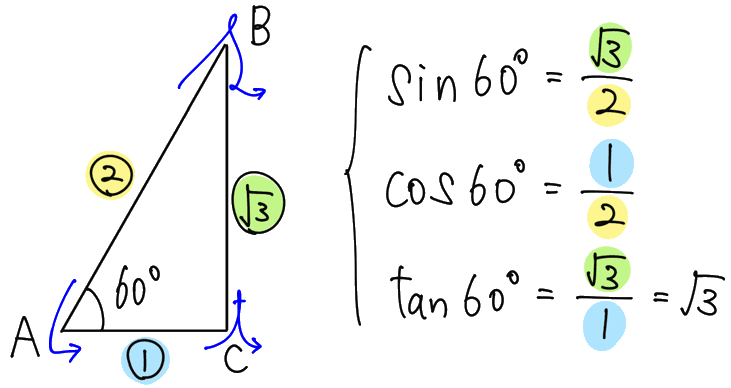
これらの2つの三角形は、向きを変えただけ、というのも意識しておきましょう！後でまた出てきます。

次に、下の45°-45°-90°の直角三角形を考えてみましょう。∠A に注目すると、それぞれの辺の比から45°の三角比が求められます。

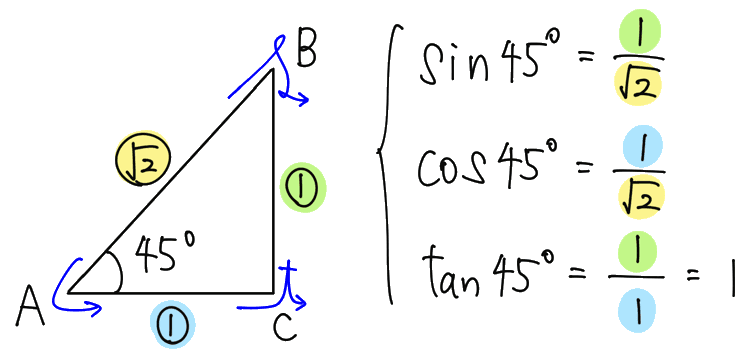
このように、まずは sin, cos, tan の定義から、30°, 45°, 60°の三角比をすぐに思い出せるようにしておきましょう。この、自力で思い出す作業を繰り返すことによって、忘れない知識となっていきます。

三角比の公式

では、この定義をもとにして、公式をいくつか解説していきます。形で丸暗記しようとせず、初めのうちは自力で思い出せるようにしつつ、自然と覚えていくようにするのが上達への近道です！

90°-A の三角比

直角三角形の直角ではない1つの内角の大きさを A とおくと、もう一つの直角ではない内角の大きさは 90°-A となりますね。

このとき、Aの三角比と90°-Aの三角比には関係があり、次の公式が成り立ちます。

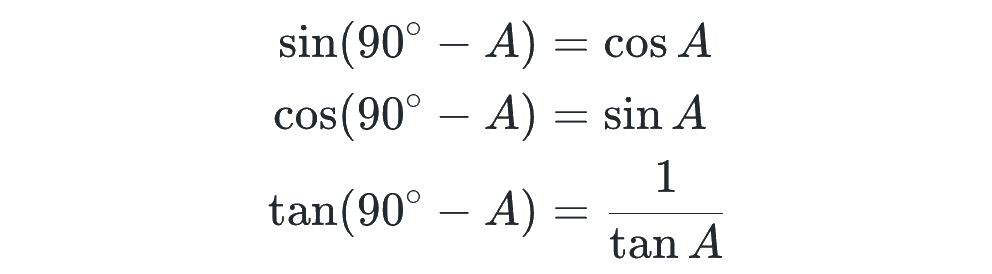
上で、30°-60°-90°の同じ直角三角形から、30°と 60°の三角比を考えたことを思い出すと、これらが成り立つ理由もわかります。

つまり、Aの三角比と90°-Aの三角比は、直角三角形の向きを変えて考えているようなイメージになるので、下の図のような関係が成り立つのです。

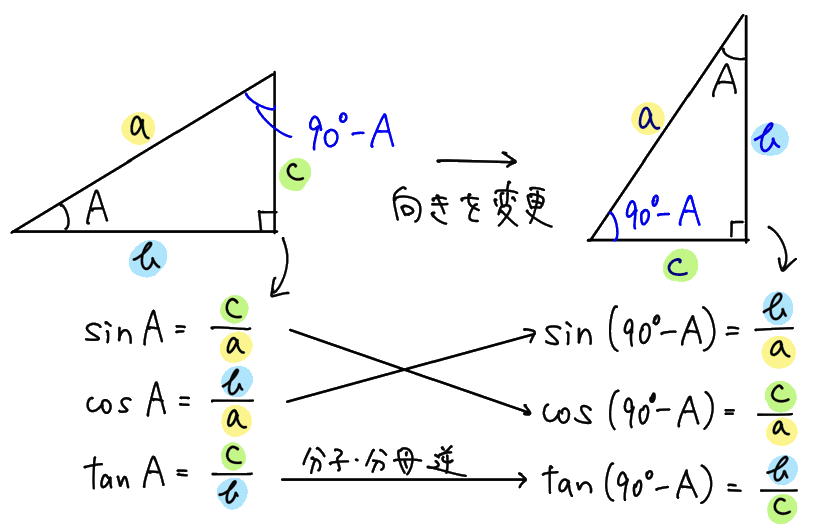
確かに、30°と 60°の三角比の値を具体的に見てみると、この関係が成り立っていますね。

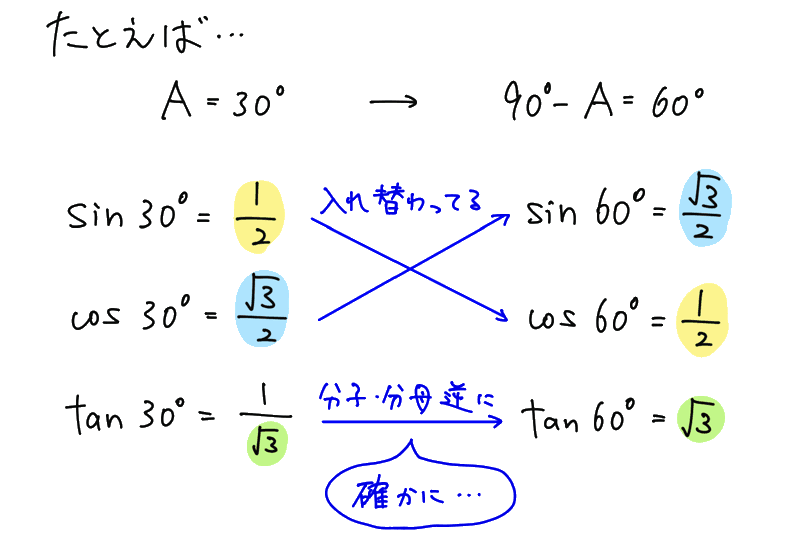
これも、直角三角形を書いて、自分でいつでも思い出せるようにしておきましょう！

ちなみに、大きさ A の角に対して、大きさが 90°-A となる角を「余角」と呼ぶので、この関係式は余角の公式と呼ばれることもあります。

三角比の相互関係

では次に、相互関係の式について学びましょう。

まず、A の値によらず、sin A, cos A, tan A について必ず以下の関係式が成り立ちます。

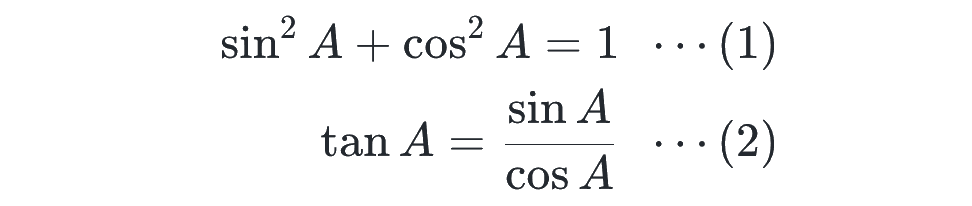
ちなみに、sin A という値の 2 乗を表すときは、「sin²A」と、sin の右上に 2 をつけます！これは、sin A² と、A の右上に 2 をつけると、(sin A)² なのか、sin (A)²（つまり A の 2 乗の sin）なのか区別ができなくなってしまうためです。最初は違和感がありますが、すぐに慣れます。

(1) (2) 式が成り立つ理由は、それぞれの三角比の定義と、三平方の定理を考えるとわかります。

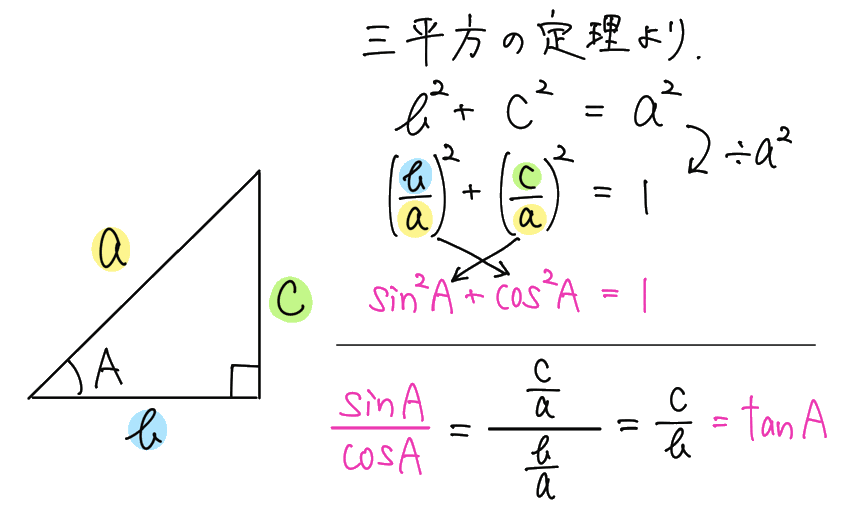
さらに、(1) (2) を使って変形したこの式もよく使います。

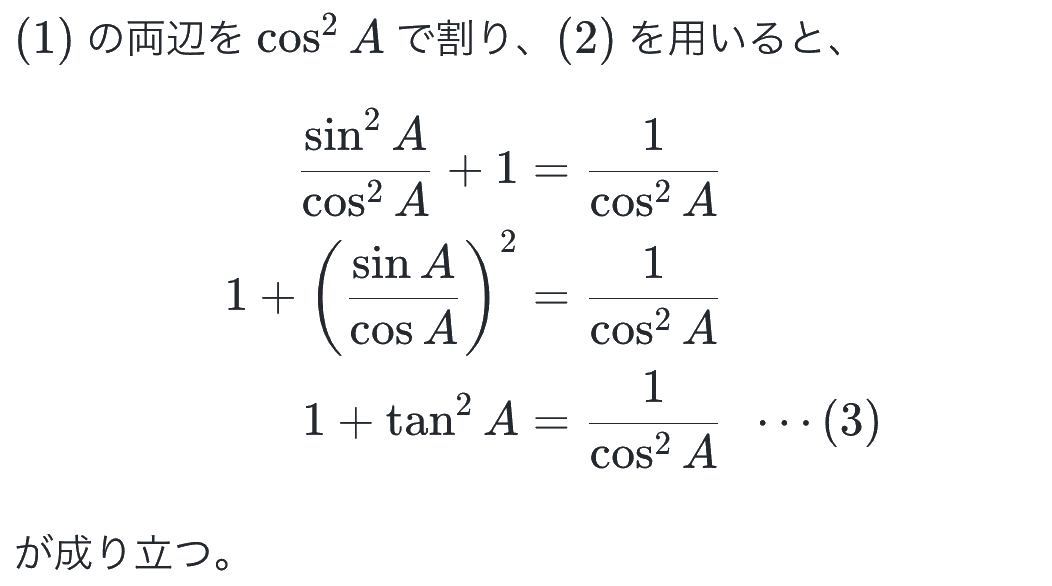
これら3本は、忘れたらいつでも作れるようにしつつ、使ううちにセットで覚えていきましょう。使い方も重要で、

• (1)式は sin と cos の関係式で、どちらかを知りたいときにもう片方から求めることができる

• (2)式は sin と cos から tan を求めるという使い方が多い

• (3)式はcos と tan の関係式で、どちらかを知りたいときにもう片方から求めることができる

というイメージです。

今は、A が 0°〜90° の場合で考えていますが、下の三角比を拡張した場合も含め、実はどんな値であっても成り立ちます。これらは、数学Ⅱの「三角関数」の分野でも再び登場する式なので、必ず押さえておきましょう。

では次のセクションに入る前に、まずはここまで学んだ三角比の基本知識の復習として、問題を解いてみましょう！（答えがすぐ下にあるので注意）

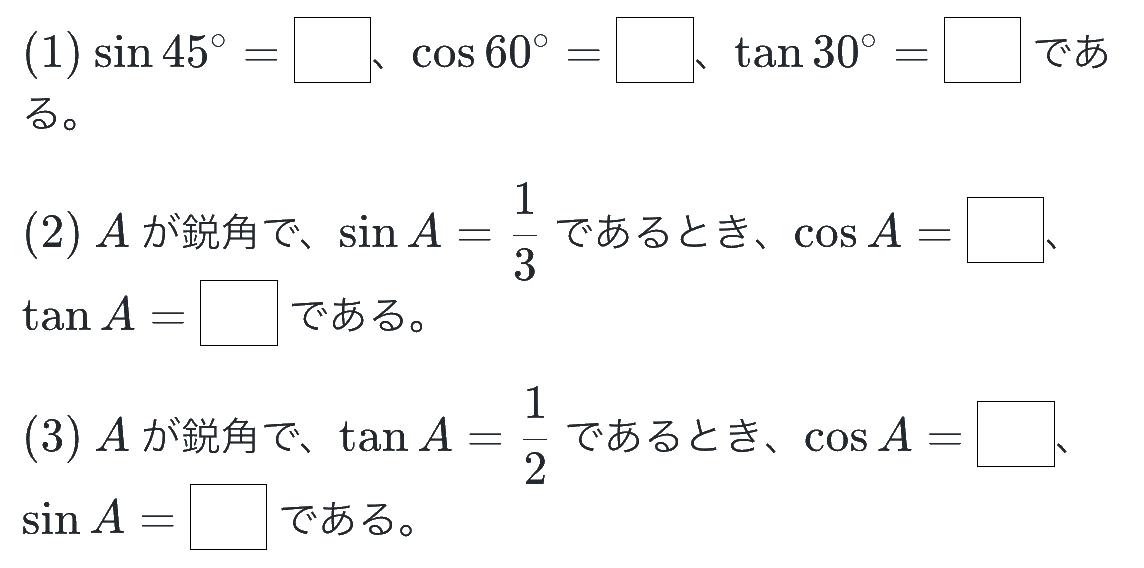
※弊社サービスのチェックテスト作成ツール「Dr.okke」より引用。1分でチェックテストが作れます。

答：(1) 1/√2・1/2・1/√3　(2) 2√2/3・√2/4　(3) 2√5/5・√5/5

三角比の拡張

上では、直角三角形による三角比の定義を学びましたが、それでは0°〜90°しか考えることができないため、ここではより広い角度で定義できる方法を考えていきます。

それが単位円（半径が1の円）を用いた考え方です。x軸正の向きから測った角度 θ（シータ）（時計回りを正、反時計回りを負とします）が決まると、それに対応する単位円上の点が1つに決まるので、その点に対して、

• y座標を sinθ

• x座標を cosθ

• 動径の傾きを tanθ

と定めます。（動径とは、単位円の中心から、その点の方向へ伸びる半直線のこと）

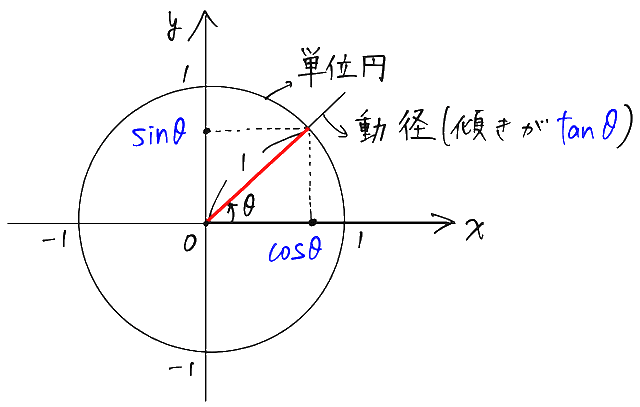
※ 拡張したことがわかるように、以下、角度は θ（シータ）で表すことにします。

ちなみに、単位円の半径は 1 なので、このように定義しても、0°〜90° の場合は直角三角形による三角比の定義と同じになることを確認しておきましょう！これを知っておくと、「sin は y 座標だっけ？x 座標だっけ？」とわからなくなったときに思い出しやすくなります。

代表的な三角比の値まとめ

0°〜180° の範囲での、よく出てくる三角比の値をまとめるとこちらです。これらはノーヒントで思い出せるようにしておく必要があります。

丸暗記すべきかどうかは、人によって言うことが違うと思いますが、とにかく大事なのは、直角三角形や単位円による定義から、いつでも全て自力で思い出せることです。特に最初のうちは、すぐに教科書などを見て値を確認するのではなく、必ず自分で考えて思い出すくせをつけるようにしましょう。そうしないと、いざというときに思い出せなくなるので注意です！！

また、

• tan 90° は定義されない

• 上の表では、わかりやすいように分母にもルートを残しているが、教科書によっては、分母を有理化した形になっていることもある（1/√2 = √2/2 や、1/√3 =√3/3 など）

ことも合わせて押さえておきましょう。

180°-θ の三角比

上では、 θ の三角比と 90°-θ の三角比の関係式を確認しましたが、実は、θ の三角比と 180°-θ の三角比にも次の綺麗な関係があります。

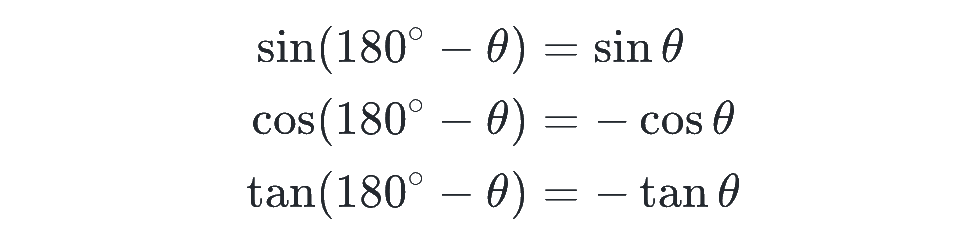
これは、以下のように単位円で考えるとすぐに思い出せます。A に対応する点と、180°-A に対応する点が、単位円上で左右対称のところに出てくるというのがポイントです！

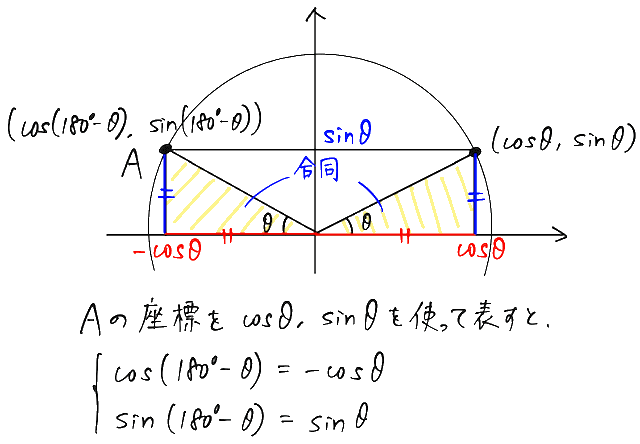
ちなみに、大きさ A の角に対して、大きさが 180°-A となる角を「補角」と呼ぶので、この関係式は補角の公式と呼ばれることもあります。

ではここで、最後のセクションに入る前に、知識が定着しているかの確認として問題を解いてみましょう！（答えがすぐ下にあるので注意）

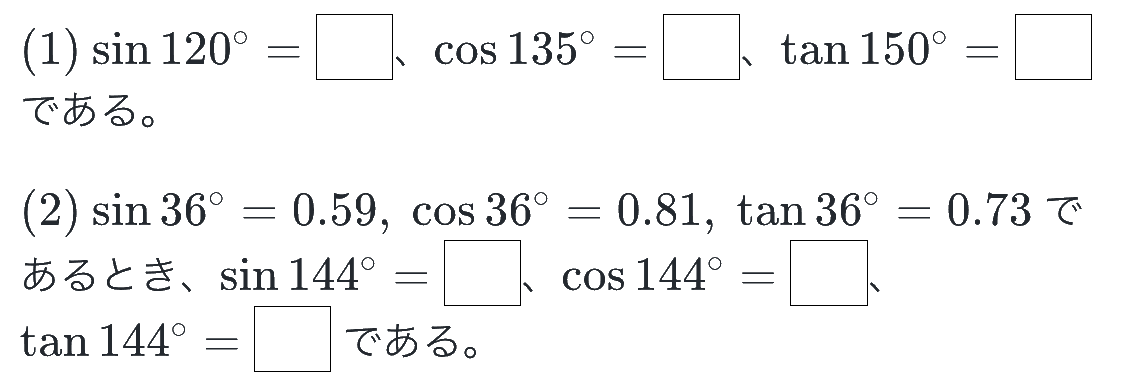
※弊社サービスのチェックテスト作成ツール「Dr.okke」より引用。1分でチェックテストが作れます。

答：(1) √3/2・-1/√2・-1/√3　(2) 0.59・-0.81・-0.73

三角形への応用

では、ここまで学んできた三角比というものを使いながら、三角形の辺や角の間に成り立つ関係を見ていきましょう。

正弦定理

3辺の長さが a, b, c で、それぞれに向かい合う角の大きさが A, B, C であるとき、三角形の外接円（3つの頂点を通る円）の半径を R とおくと、下の関係式が成り立ちます。

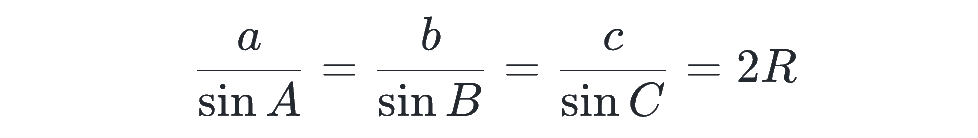
文字が多いですが、こんなイメージです。

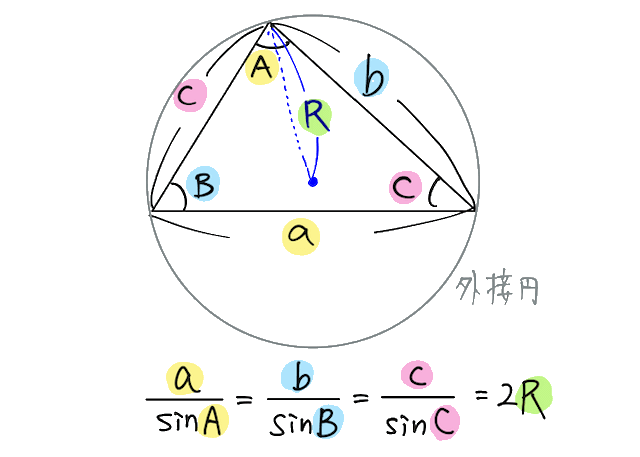
分子と分母がどっちかを忘れたり、外接円の半径に2を掛け忘れたりしやすいので、問題を解きながら確実に覚えていきましょう！ちなみに、sin（正弦）が出てくるので「正弦定理」といいます。

この正弦定理は公式の使い方が大事で、使う場面としてはだいたい下の 2 パターンです。

• 対応する 1 組の辺と角（例：a と A）と、他の辺か角が 1 つわかっているとき（例：b や B）に、その対応する角か辺（例：B や b）を求めることができる

• 対応する 1 組の辺と角（例：a と A）から外接円の半径 R を求めることができる

定理の証明はここでは省略しますが、特にこの正弦定理の証明では、さまざまな図形の知識が登場して、とても良い復習になるので、わからない方はぜひ授業動画などで確認しておきましょう！（正弦定理の証明の授業動画まとめ（okkeで検索））

余弦定理

では次に、cos（余弦）についての定理である、余弦定理を見てみましょう。

3辺の長さが a, b, c で、それぞれに向かい合う角の大きさが A, B, C であるとき、下の関係式が成り立ちます。

角度について求めたいときには、cos について整理した下の形をよく使います。

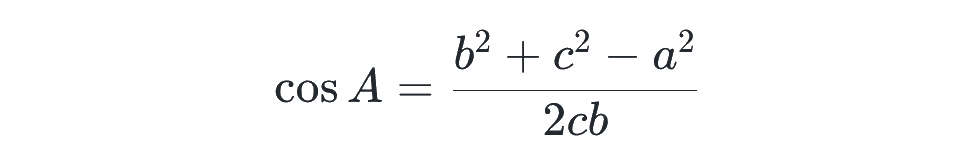
文字が多いですが、こんなイメージです。

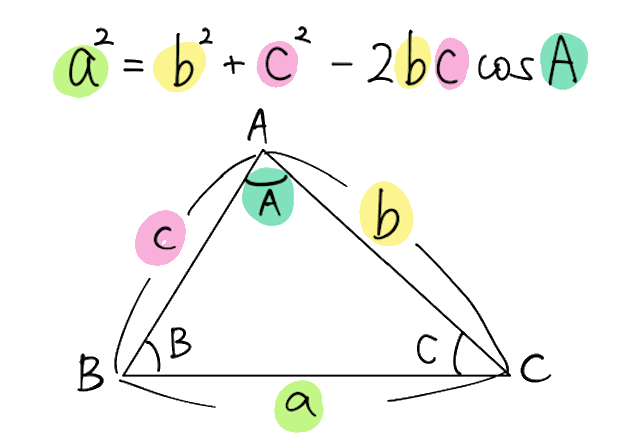
こちらの余弦定理も公式の使い方が大事で、使う場面としてはだいたい下の 2 パターンです。問題を解きながらコツをつかんでいきましょう。

• 2 辺とその間に挟まれた角がわかっているときに、残りの辺の長さを求めることができる

• 3 辺がわかっているときに、ある角の cos を求めることができる（どの角でもOK）

※ 他の角（B や C）についても全く同じように成り立ちますので、これらの使い方がわかっておけば他の 2 つのバージョンの式は覚える必要はありません。

定理の証明はこちらも省略しますが、とても大事なので、わからない方はぜひ授業動画などで確認しておきましょう！（余弦定理の証明の授業動画まとめ（okkeで検索））

三角形の面積

三角形の面積の求め方は、中学まででは基本的に「底辺×高さ÷2」でしたが、三角比を用いると、2つの辺と、それらにはさまれた角の sin が分かれば、このように面積を求められます。

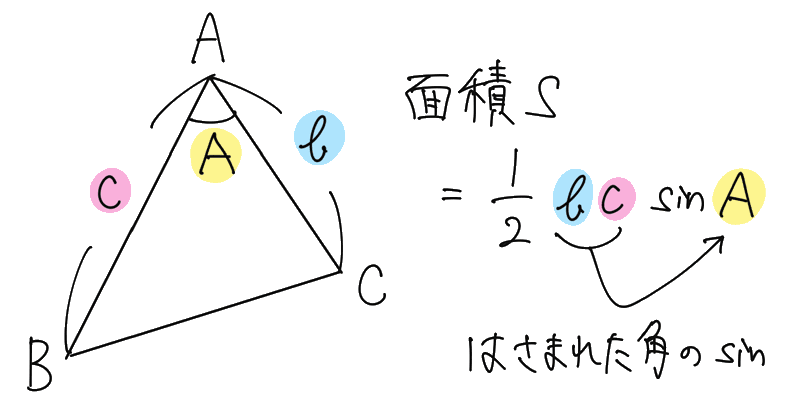
角 A が直角であっても鈍角であっても、これで求めることができます。

正弦定理や余弦定理と並び、こちらの公式もこのあとずっと登場してくるので、確実に押さえておきましょう。

証明はこちらも省略しますが、例えばこのokke用語のページを見て確認しておきましょう。

※ 他の角（B や C）がはさまれた場合についても、全く同じように、2つの辺と、それらにはさまれた角の sin を掛ければ面積が求められます！

では、ここまで出てきた公式の知識が定着しているかの確認として、問題を解いてみましょう。（答えがすぐ下にあるので注意）

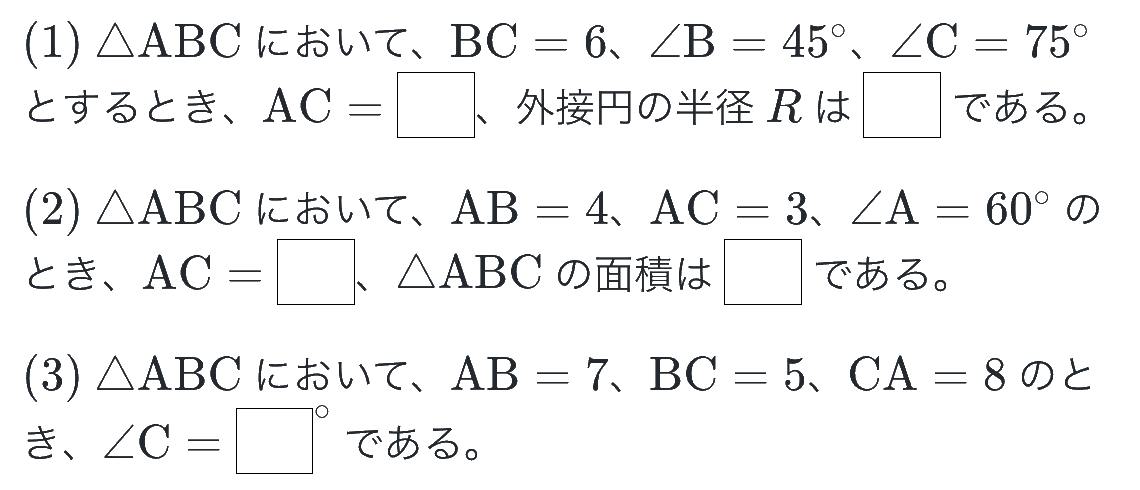
※弊社サービスのチェックテスト作成ツール「Dr.okke」より引用。1分でチェックテストが作れます。

答：(1) 2√6・2√3　(2) √13・3√3　(3) 60

三角比をマスターできる参考書を紹介！

三角比をマスターするためには、

• 定義から基本的な三角比の値を出せるようにすること（すぐにその場で思い出せるようにしていくことが大切、方程式や不等式などの逆算も重要）

• 相互関係の式を自在に使いこなせるようにすること

• 三角形と絡めた公式を、使う場面の見極めも含めて習熟すること

という3つの大きなステップがあるので、これに沿って進めていくのが良いでしょう。

どのステップにおいても、定義や公式をその場で自力で思い出して、正しく使えるようにするためには、どうしても演習の量が大切になりますので、基本的には学校で配布される4STEPなどの傍用問題集や、チャート式などの網羅的な問題集といった、問題数の多い参考書に取り組むのがおすすめです。

その後、応用的な問題を解いていく段階では、知識を整理しながら進めることも大事になりますので、解説が詳しい参考書を用いるのがオススメです。

ここでは、三角比の演習量を確保しつつ、理解を深めるのにピッタリな参考書・問題集をいくつかご紹介しますので、参考書を買う際の参考になれば幸いです。

※ なお、教科書や参考書の目次の単元名としては、「三角比」ではなく「図形と計量」が一般的ですので、注意してください！

苦手な方向け

• 坂田アキラの三角比・平面図形が面白いほどわかる本 (坂田アキラの理系シリーズ)（坂田アキラ、KADOKAWA出版）

単元のピンポイントな学習に最適な、数学Ⅰの三角比と、数学Aの平面図形の分野に特化した参考書です。三角比の基礎から丁寧に解説されているので、苦手な方や、学校の授業について行けなくなってしまって復習したい方に向いています。

また、三角比は数学Aの平面図形の分野とつながる内容も多いので、一緒に学ぶことで効率よく進めることができます。

• 数学Ⅰ・A 入門問題精講（池田洋介、旺文社）

この参考書は、問題演習のみならず、各単元の導入から詳しく解説されているのが大きなおすすめポイントです。各単元の内容を理解した上で、取り組みやすい問題かつわかりやすい解説で知識を定着させていけるので、先取り学習や、弱点克服にとても役に立ちます。

数学ⅠAの他の単元も含まれますが、三角比の部分だけ取り組む、といったピンポイントな使い方もおすすめです。

公式を覚えて次のレベルに進みたい人向け

• 数学Ⅰ・A 基礎問題精講（上園信武、旺文社） 

公式は覚えたし、教科書的な知識はあるのに、いざ模試などのテストになると三角比の問題が解けない方にとてもオススメの参考書です。厳選された良問を通じて、問題を解く上でのポイントを学べます。問題数もそこまで多くないので、三角比だけガッと1週間で強化する、といった使い方も可能です。

難関大レベルまで実力を伸ばしたい方向け

• 理系数学の良問プラチカ 数学ⅠAⅡBC (河合塾シリーズ 入試精選問題集 5)（大石隆司、河合出版） / 文系数学の良問プラチカ 数学ⅠAⅡBC(河合塾シリーズ 入試精選問題集 4)（鳥山昌純、河合出版）

応用レベルの頻出テーマが必要最小限の問題で網羅されており、解説も詳しいので、得点源にしたい場合には、これらの中の「図形と計量」の範囲の問題を解いていくと効率が良いです。記述模試や実際の入試問題でよく見かけるテーマが凝縮されているので、模試や過去問になると解けなくなる方などにもおすすめです。

※「理系数学のプラチカ」よりも、「文系数学のプラチカ」の方が難しいので、注意してください。最難関大を目指す方以外は、文系の方であっても「理系数学の良問プラチカ」を使うのがおすすめです！

演習量を増やし、知識を確実に定着させるならDr.okke

三角比の分野では、定義・公式の定着や、問題のパターンへの慣れがとても重要ですが、参考書では、すぐに下のポイントから必要な知識が見えてしまったり、一度解いてしまうと「ここのページはこの解法だな…」と、問題の場所から公式や解法が推測できてしまったり、そもそも問題の解答を覚えてしまったりと、定着度の確認や効果的な反復演習を行うことが難しい場合も多いです。

そこで新しいテスト作成ツールであるDr.okkeをご紹介いたします。

いつでもすぐにテストを作成・実施

• 教科書の内容確認レベルの基礎から大学入試レベルの応用問題までを網羅しており、今日の授業でやったテーマに絞ったチェックテストから、分野を混ぜた実力テストまで、全て1分で簡単に作成可能です。

• 計算の一行問題に特化した「計算ドリル」という科目も別で用意しており、三角比の定義・公式の運用や計算力をとにかく鍛えるといった使い方も可能です。

• 充実した良問とシャッフル出題によって、三角比のそれぞれの公式や使い方を定着させられているかを確実にチェックできます。公式の数が多く、その定着が土台になる三角比の力を引き上げるには、まさにピッタリのツールです。

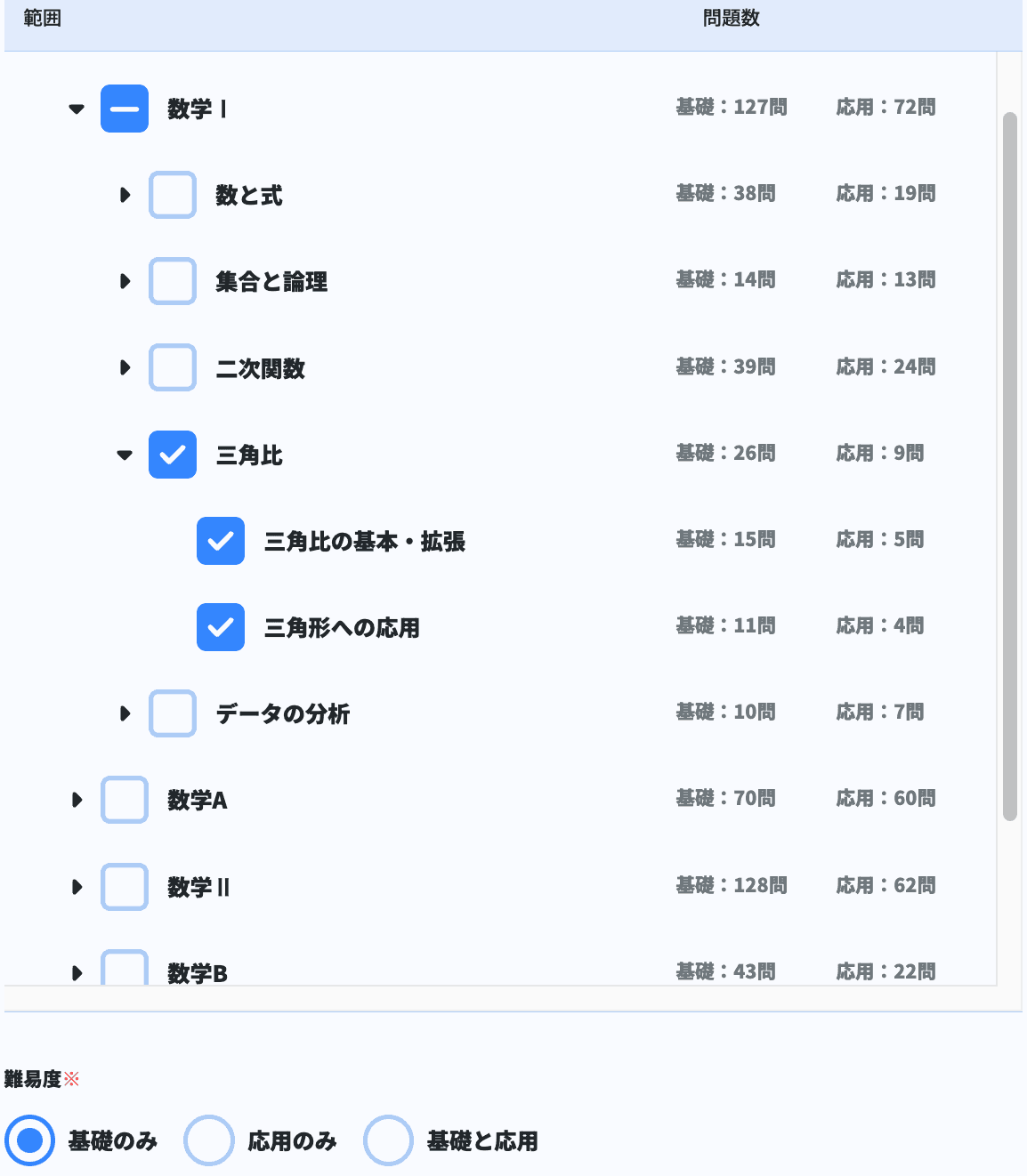
※ 難易度調整、制限時間設定も簡単にできます。

 自動採点かつ、受験結果のデータが蓄積

• テストを受けた直後に結果が表示され、解説も手作りでかなり詳しく作っているため、疑問を残さず、理解も深められます。

• 受験結果がデータとして自動で蓄積されるので、生徒さんの理解度や今復習すべき単元などが一目で分かります。これからのカリキュラムや学習計画を立てる際に、より一人ひとりに寄り添った指導を実現することができます。

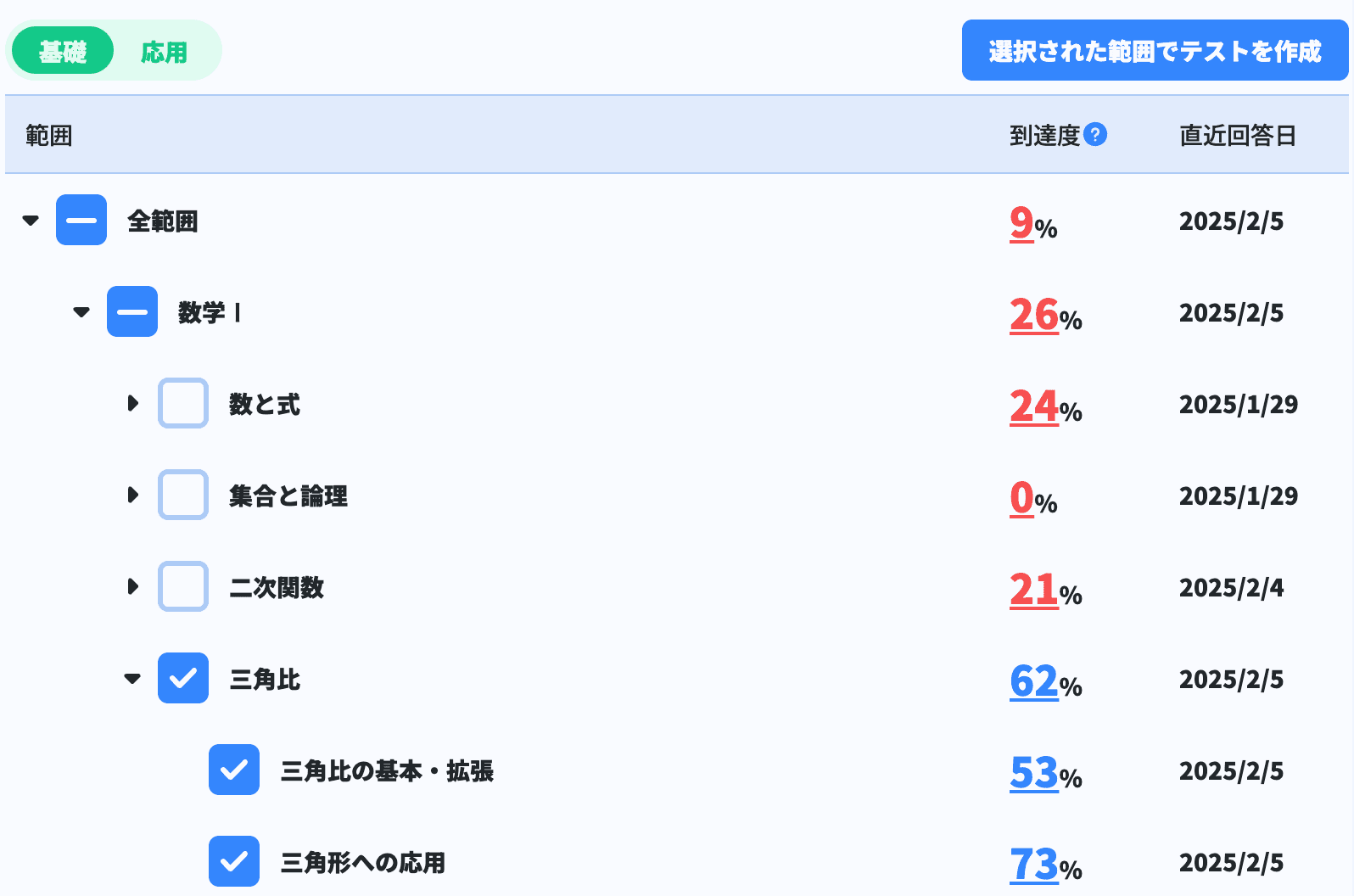
無料体験期間もありますので、ぜひ一度お試しください。

Dr.okkeの導入をご検討の方は、こちらの画像をタップし、無料トライアルをお試しください！確認テストはDr.okkeにおまかせください！

まとめ

この記事では、三角比（図形の計量）の単元で出てくる定義や公式を、思い出し方を含めて総まとめするとともに、おすすめ参考書を紹介しました。公式がたくさん出てきますし、公式だけ頑張って覚えても、いざ問題を解こうとすると、どの式を使えば良いか戸惑ってしまうことが多く、苦手な方にとっては高い壁となりがちな単元です。

そこで学習の際にとても大切になるのは、公式を忘れてもすぐに思い出せるよう、普段の演習のときから「自力で作るクセ」をつけておくことと、自分の理解度に合った解説の詳しい参考書を選び、内容をしっかり理解した上で、その公式がどのような場合に使えるのかを合わせて押さえていくことです。毎回教科書の公式を見ながら問題を解いていては、いつまで経っても公式を思い出すことはできません。

また、使う式がわかって式が立てられても、計算力が無いと正答できないため、普段の演習から最後まで自分の手で計算するようにすることが重要です。

上で紹介したように、解説の詳しい市販の参考書や問題集もたくさんありますが、問題の並びで使う公式や解法が推測できてしまったり、最後まで解き切らず、解法だけ合っていたら先に進んでしまったりと、どうしても効果的な学習ができないこともあります。その際には、Dr.okkeのようなテストツールを有効活用し、定着させられているかを確認しながら着実に学習を進めていくことが、三角比の得点アップへの近道となるでしょう。（もしDr.okkeにご興味がありましたら、こちらまでご連絡ください。無料トライアル実施中です！）

三角比は、新しい概念が登場して手強い単元ですが、数学Ⅱの三角関数にそのままつながっていきますし、数学Aの図形の性質や数学Cのベクトルなど、関連する単元も多いため、ぜひ得意にしておきたい単元です。この記事を参考に苦手意識を克服し、試験本番で確実に解けるように効果的に学習に励んでいきましょう。