作成日:
2025/02/20
更新日:
2025/10/17
はじめに
指数関数(指数の拡張・指数関数とグラフ)は、教科書でのページ数が少なく、学校の授業でもさらっと通り過ぎることも多いと思いますが、新しい定義がたくさん出てくるので、慣れていかないとそもそも何をやっているのかがわからず、苦手な方にとってはつらい単元になりがちです。
そこで、この記事では、指数関数の単元で出てくる定義や公式を、思い出し方やコツも含めて詳しく一気に解説するとともに、しっかりと理解して解けるようになるためのおすすめ参考書を紹介しました。
新しい定義が登場して手強い単元ですが、模試や受験でも頻出ですし、理系の方は数学Ⅲでもたくさん登場するテーマであるため、ぜひ得意にしておきたい単元です。また、量自体は少ない分、短期間で仕上げることも可能なので、この記事を参考に、効果的に学習に励んでいきましょう。ぜひ最後まで読んでみてください!
指数の拡張
指数法則の復習
このあとたくさん使うので、まずは数学Ⅰの「数と式」の単元で学ぶ指数法則を復習しておきましょう。
m, n を正の整数(自然数)とするとき、以下の式が成り立ちました。
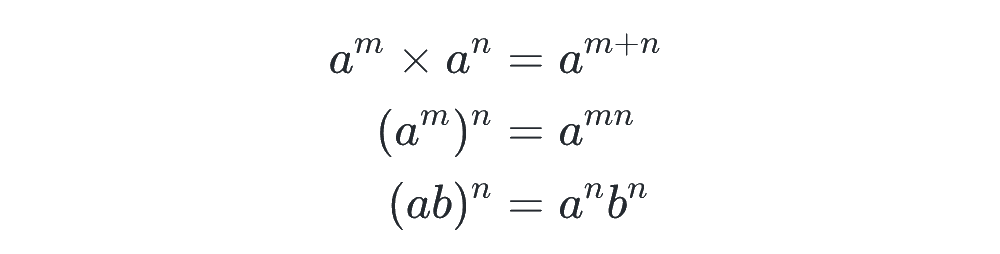
これは、実際に掛け算の形で書いてみると、成り立つ理由がわかりやすいです。
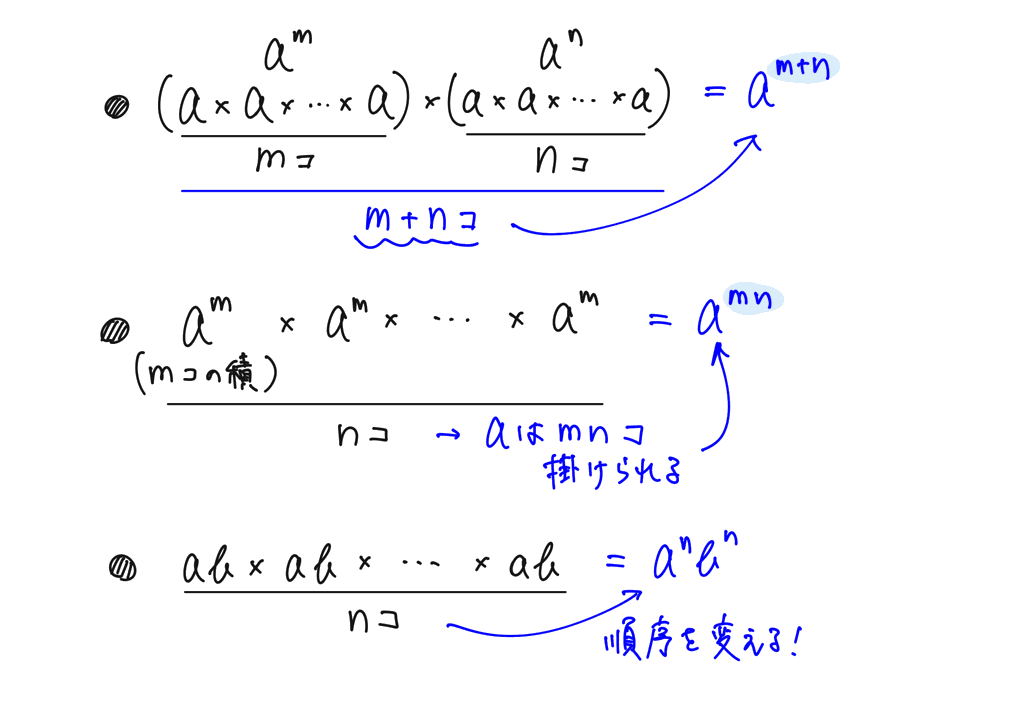
ちなみに、指数というのは右肩に乗っている数字のことです。
実はこの後見ていくように、この指数法則は、指数の m, n を自然数に限定しなくても、指数が実数の場合に成り立ちます。というよりも、この指数法則が実数全体で成り立つように、指数を 0、負の整数、分数(有理数)の場合に拡張させたときの累乗を定義していきます。
以下、それぞれの場合に分けていきましょう。
指数が0または負の整数のとき
指数が0または負の整数のときの累乗を、以下のように定めます。(a≠0、n は正の整数(自然数)とします)
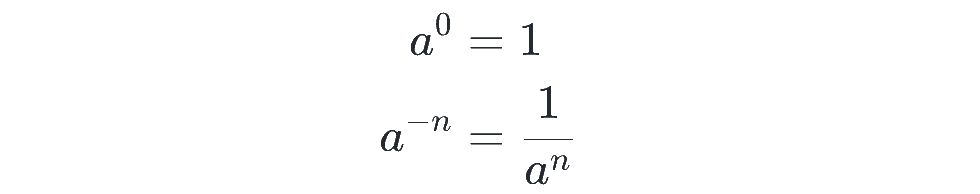
これは、指数が 1 増えるごとに a 倍、1 減るごとに 1/a 倍されることを考えると、自然に感じられると思います。
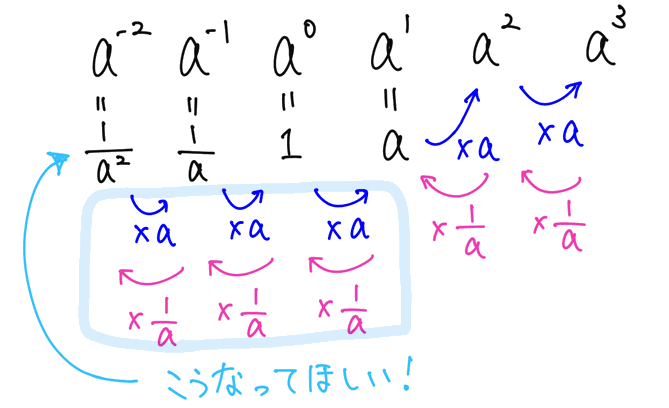
このとき、この定義を用いると、指数が0や負の整数であっても、指数法則が成り立つことを確認しましょう。
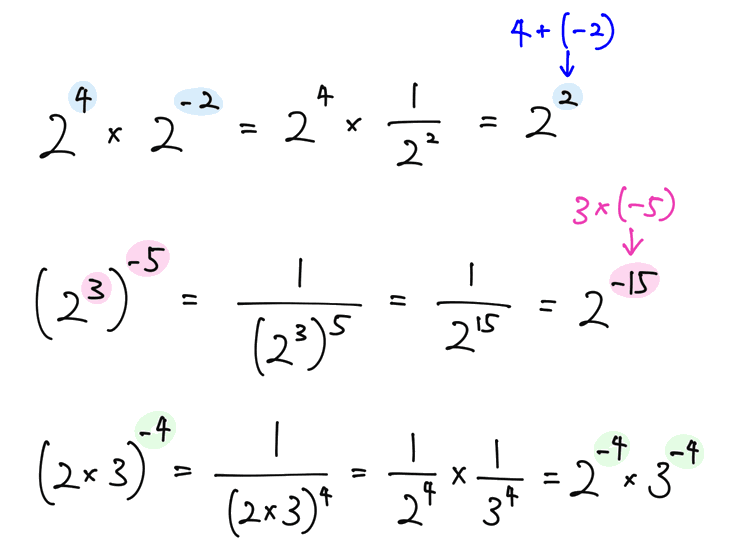
累乗根とは
指数をさらに拡張させて、分数(有理数)のときを考える前に、累乗根というものについて学んでおきましょう。
方程式
の解のことを、実数 a の n乗根といいます。簡単にいうと、n 回かけて a になる数のことです。
※ 複素数の範囲を含めると、実数 a の n 乗根は n 個存在するのですが、ここでは実数の範囲で話を進めましょう。
例えば、4 の 2乗根は ±2(2つ)、-27 の 3乗根は -3(1つ)です。
2乗根、3乗根、4乗根、... のことをまとめて累乗根といいます。
ここで、実数 a の n乗根について、以下のように定義された記号(ⁿ√a)を考えます。ルールがややこしいので、苦手な人はとりあえず、ルート(平方根)と同じようなもので、n 回かけて a になる数を表してるんだ、くらいに思っておけば大丈夫です。

n の偶奇で場合分けが必要ですが、どちらの場合でも、値がただ 1 つに決まるように記号を定義しているのがポイントです。それぞれの場合を、例で理解しましょう!
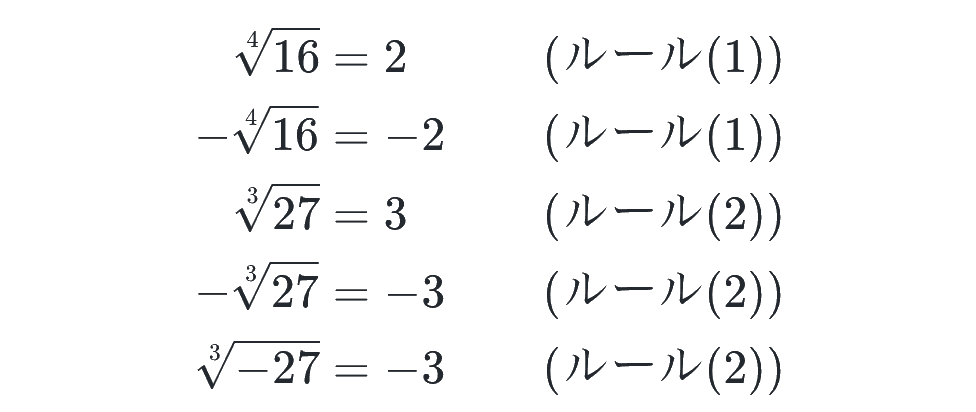
※ ⁿ√a はあくまでも 上の定義に沿った 1 つの値であり、2行目と4行目のように、それにマイナスがついたら値もマイナスになります!
ちなみに中学校からおなじみの「ルート(平方根)」は2乗根のことで、左肩の小さい 2 は省略されていますが、累乗根の仲間です。
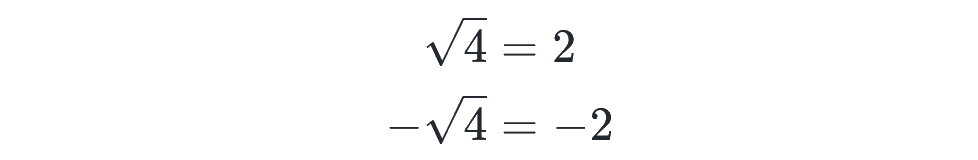
このように、確かに累乗根の定義通りですね。上が正のルート(4 の 2乗根)、下が負のルート(4 の 2乗根に、マイナスをつけたもの)と呼ばれます。
累乗根については、ルートと同じように以下の性質が成り立つので、押さえておきましょう。(a>0、b>0、m と n は正の整数(自然数)とします)
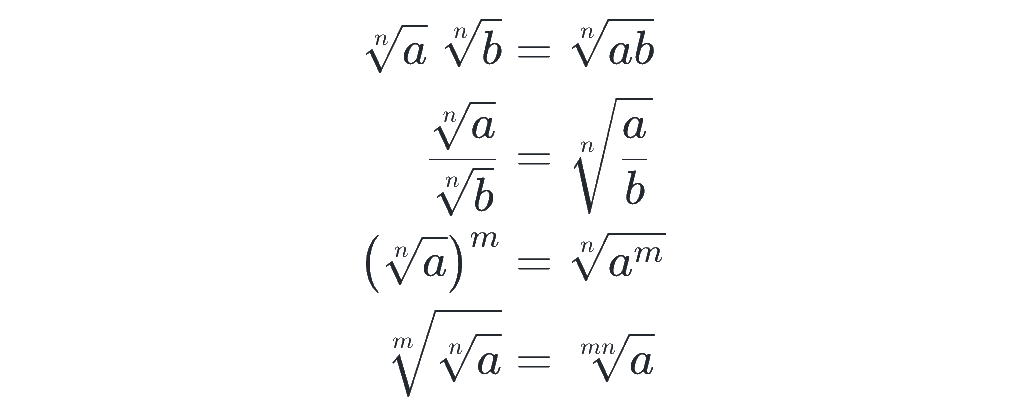
指数が分数(有理数)のとき
では、指数をさらに拡張させて、分数(有理数)のときを考えましょう。
指数が分数(有理数)のときの累乗は、累乗根を用いて以下のように定められます。(a>0、m は整数、n は正の整数(自然数)とします)
指数が分数(有理数)であっても指数法則が成り立つとすると、例えば
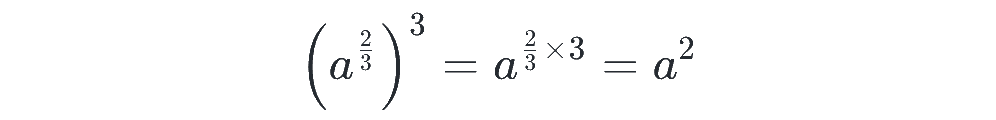
となりますが、これは、最初の式と最後の式を見れば、aの3分の2乗が、a²の3乗根であることを表しているので、確かに累乗根を用いて
で定めると良さそうであることがわかりますね。
指数が分数(有理数)のときの定義と、指数が分数であっても指数法則が成り立つことを必ず押さえておきましょう!
では次のセクションに入る前に、まずはここまで学んだ知識の復習として、問題を解いてみましょう!(答えがすぐ下にあるので注意)
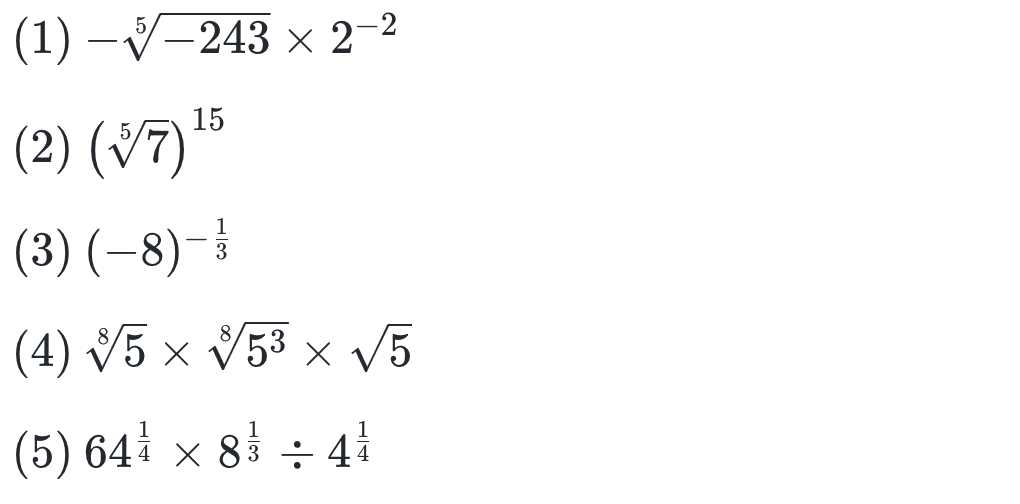
※弊社サービスのチェックテスト作成ツール「Dr.okke」より引用。1分でチェックテストが作れます。
答:(1) 3/4 (2) 343 (3) -1/2 (4) 5 (5) 4
指数関数とそのグラフ
指数関数とは?
上では、指数が有理数の場合まで確認しましたが、実は、√2 のような無理数が指数となったときも、以下のように近づいていく一定の値として定めることができます。

つまり、実数全体の場合に定義できたことになるので、実数 x を 1 つ決めれば、2ˣ の値はただ 1 つに決まることになります。よって、y=2ˣ という「関数」を考えることができます。このような関数のことを指数関数と呼びます。一般に、a>0、a≠1 のとき
を指数関数といい、a のことを「底」(てい)といいます。
※ x を 1 つ決めたときに、y が「ただ 1 つ」に決まるものを関数といいます。
指数関数のグラフ
では、この指数関数のグラフを考えていきます。
まず、底を 2 とした、y=2ˣ のグラフを考えてみましょう。
いくつかの x を具体的にとり、2ˣ の値(y の値)を計算してみると、以下のようになります。
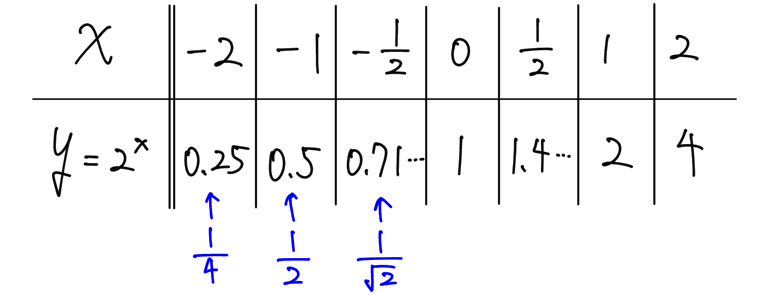
※ グラフの形が重要なので、とりあえず、整数のときの値は頭で計算できるようにしておきましょう。
これを座標平面にとっていくと、下のような曲線が描けます。これが y=2ˣ のグラフです。y が正の値をとりながら、右上がりになるのがポイントです。
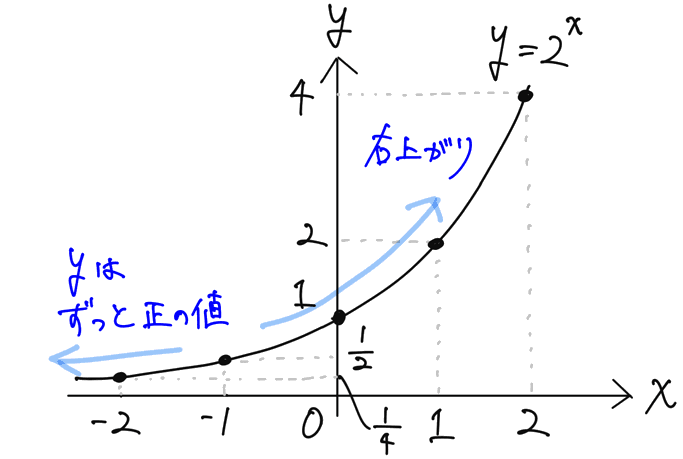
次に、底を 1/2 とした、y=(1/2)ˣ のグラフを考えてみましょう。
これも、いくつかの x を具体的にとり、y の値を計算してみると、以下のようになります。
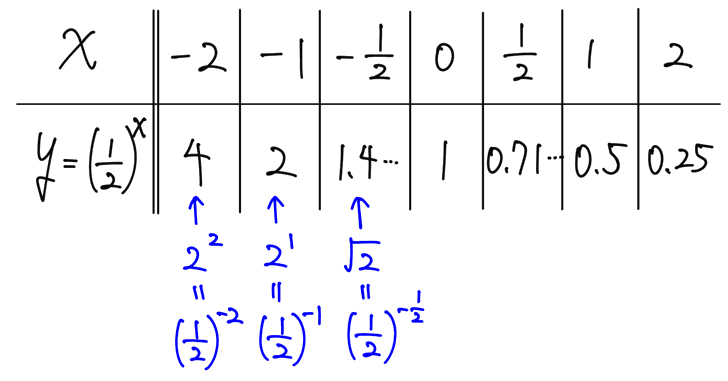
※ グラフの形が重要なので、これも、整数のときの値は頭で計算できるようにしておきましょう。
これを座標平面にとっていくと、下のような曲線が描けます。これが y=(1/2)ˣ のグラフです。y が正の値をとりながら、右下がりになるのがポイントです。
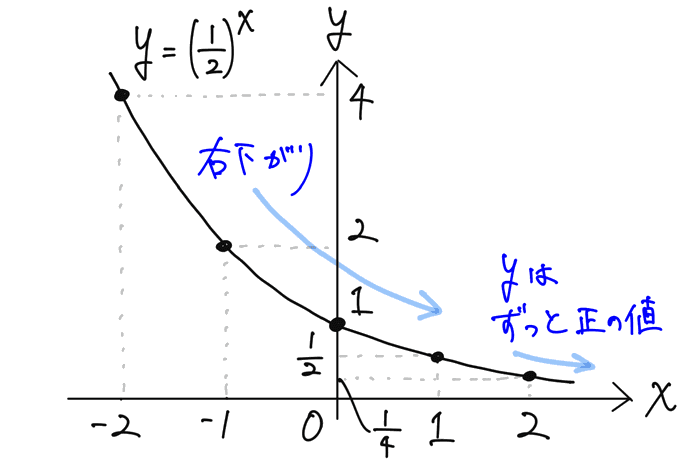
つまり、指数関数 y=aˣ のグラフのポイントは一般に以下の通りです。
定義域(x のとりうる値の範囲)は実数全体
値域(y のとりうる値の範囲)は正の実数全体
グラフは (0, 1) を通る
a>1 のとき、グラフは右上がり(x が増加すると y も増加する)
0<a<1 のとき、グラフは右下がり(x が増加すると y は減少する)
特に、底の 1 との大小によって、グラフの形が変わる点がとても重要です!
ちなみに、指数の拡張や指数法則を用いると、
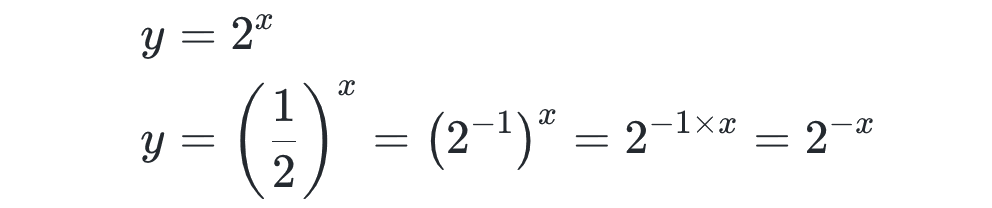
なので、お互いに x を -x に変えた形になっていて、y=2ˣ と y=(1/2)ˣ のグラフは y 軸対称となります。
指数方程式・指数不等式
指数方程式の考え方
指数関数を含む方程式(指数方程式)について、考え方を軽く見ておきましょう。テストでも頻出です。
考え方の鉄則は以下の2つです。
底が揃っていない場合には揃えてから、指数を比べられるようにする
項がいくつかある場合には、置換できないか考える
実際に解きながら見ていきます。
まずはこちらを自力で考えてみましょう。
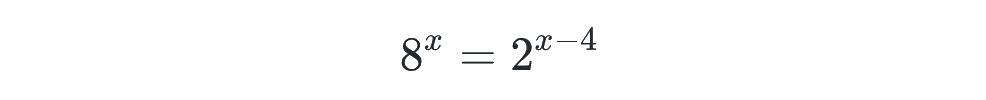
底が 8 と 2 で揃っていないので、揃えましょう。この場合、8 を 2 に揃えるのが考えやすく、左辺は
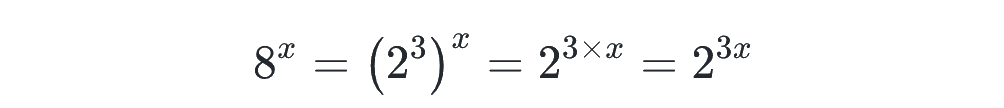
と変形できるので、方程式はこのようになります。
これで、指数を比べられる形になりました。
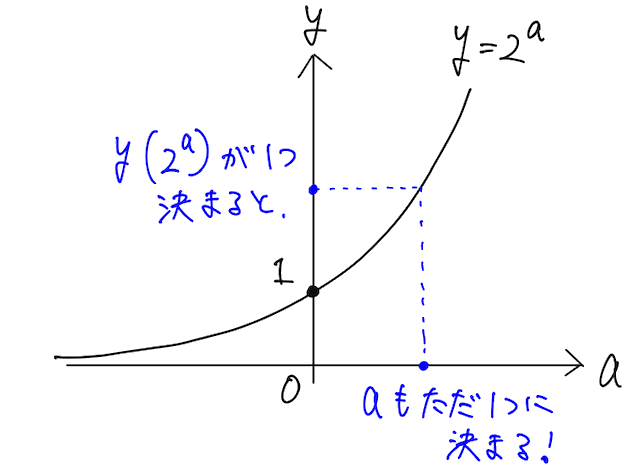
ここで、y=2ᵃ のグラフを思い出すと、y つまり 2ᵃ の値が同じであれば、a の値も同じになる(x だとややこしいので、a にしています)ので、上の方程式は、指数同士が等しいことと言い換えられて、
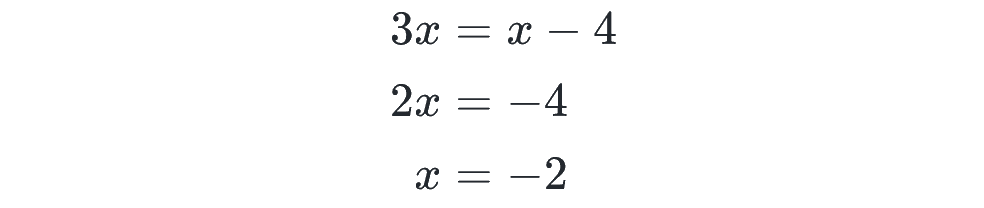
として解けます。
では次にこちらを自力で考えてみましょう。
まずは、底が 4 と 2 で揃っていないので、揃えましょう。この場合、4 を 2 に揃えるのが考えやすく、左辺は
と変形できるので、方程式はこのようになります。
ここで、考えやすいように、 2ˣ=t と置き換えます。(慣れてきたら、x のままいってももちろんOKです)
であることに注意すると、方程式は
という、t についてのシンプルな二次方程式に置き換えられました!これがポイントです。
このとき、とても重要なのが、置き換えた t にはとれる値の制限がつくということです。つまり、x のとりうる値の範囲は実数全体であったとしても、2ˣ (=t) のとりうる値の範囲は、上のグラフで考えた通り「正の実数全体」、つまり t>0 となるのです。
ですので、この二次方程式の解のうち、t>0 を満たすもののみを探しましょう。(t≦0 を満たす解については、t が求められたとしても、対応する x が存在しません)
因数分解で解くと、t>0 を満たす解 t は、
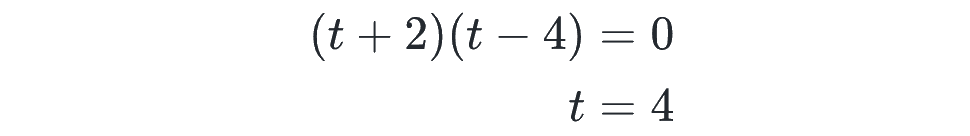
となります。(t=-2 は t≦0 なのでここでは不適です)
あとは、置き換えた式(2ˣ=t)から x の話に戻して、先ほどと同じ流れで、底を揃えつつ解 x を求めます。
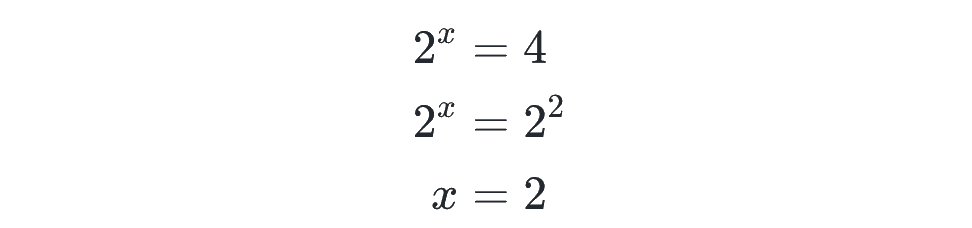
※ x は実数全体をとりうるので、マイナスの値でも解になります。t (=2ˣ) の範囲とごっちゃにならないよう注意しましょう!
とにかく、指数関数を含む方程式(や、下で出てくる不等式)では、
底が揃っていない場合には揃えてから、指数を比べられるようにする
項がいくつかある場合には、置換できないか考える
という意識を常に持っておきましょう。
指数不等式の考え方
では、指数関数を含む不等式(指数不等式)についても軽く見ておきます。方程式のときと考えるべきことは全く同じですが、底が 1 より大きいか小さいかで不等号の向きが変わるので、そこだけ注意しましょう。
実際に解きながら見ていきます。まずはこちらを解いてみてください。
底が 4 と 32 で揃っていないので、揃えましょう。この場合、32 を直接 4 のなんとか乗で表すことは少し難しいのですが、両者の底を 2 に揃えるとわかりやすく、方程式はこのようになります。
これで、指数を比べられる形になりました!
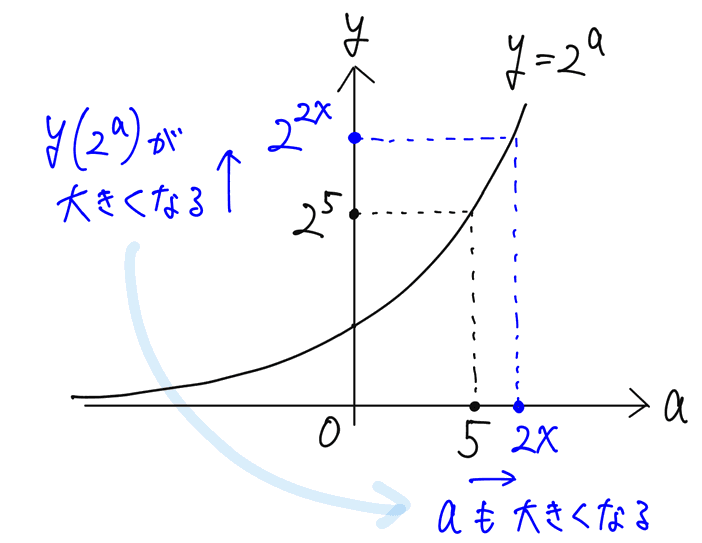
ここで、y=2ᵃ のグラフを思い出すと、y つまり 2ᵃ の値が大きくなると、a の値も大きくなる(x だとややこしいので、a にしています)ので、上の不等式の指数の大小を比べると、
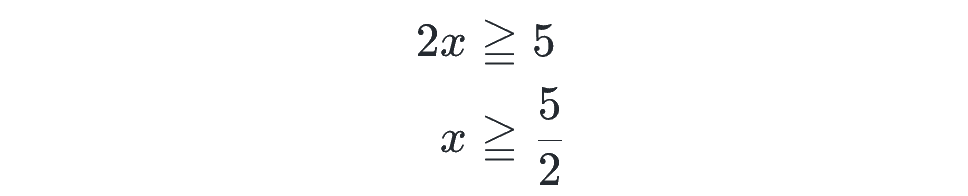
として解けます。グラフのイメージとともに必ず理解しておきましょう。
次にこちらを解いてみてください。
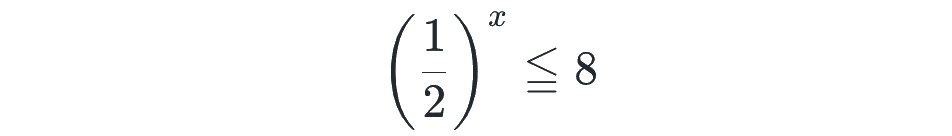
底が揃っていないので、1/2 に揃えると、
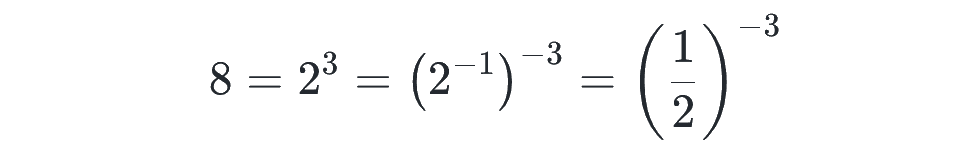
方程式はこのようになります。
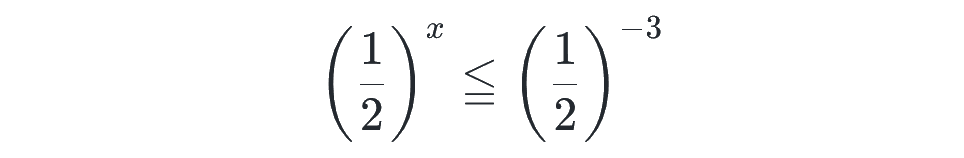
これで、指数を比べられる形になりました!
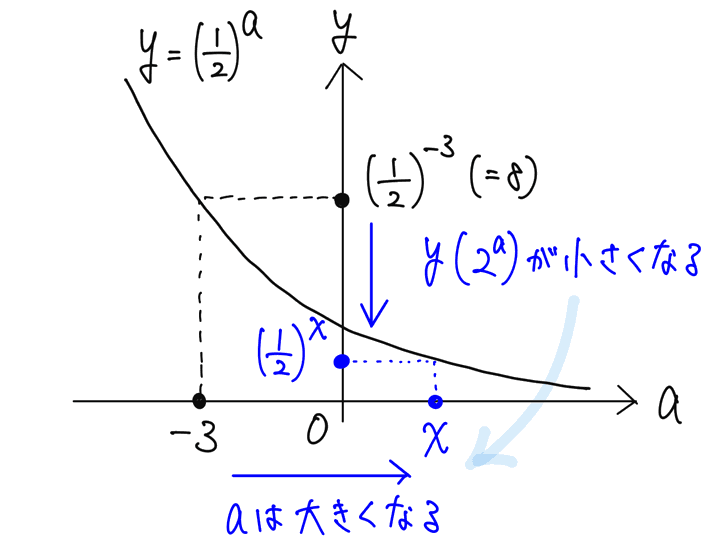
ここで、y=2ᵃ のグラフを思い出すと、y つまり 2ᵃ の値が大きくなると、a の値は小さくなる(x だとややこしいので、a にしています)ので、上の不等式の指数の大小を比べると、
として解けます。指数同士の大小関係が逆になる点に注意です。グラフのイメージとともに必ず理解しておきましょう!
※ 置換が役に立つ不等式の問題はここでは省略しましたが、これまで紹介してきた流れで解けますので、教科書や問題集で取り組んでみてください。
対数・対数関数へのつながり
ここでは詳しくは紹介しませんが、対数や対数関数へのつながりも学んでおきましょう。
指数関数を含む方程式(指数方程式)のところで考えたように、y=2ˣ という指数関数があったとき、y が正の範囲で 1 つ決まると、実数 x の値はただ 1 つに決まります。
つまり、一般に、a>0、a≠1、M>0 のとき
を満たす実数 p がただ 1 つに決まり、その p を、
という記号で表すことにします。これを、a を底とする対数といい、M のことを真数といいます。底は指数関数のときと同じものを指していますね。
この対応関係が重要なので、下のような簡単な値などでいつでも思い出せるようにしておきましょう。
さらに、正の値 M が 1 つ決まると、実数 p がただ 1 つ決まるという対応関係から、これを関数として考えることもできて、a>0、a≠1 のとき
で表される関数のことを、a を底とする対数関数といいます。(定義から、真数 x のとりうる値の範囲(定義域)は x>0 であることに注意です。これを真数条件といいます)
指数関数をマスターできる参考書を紹介!
指数・指数関数をマスターするためには、
累乗根や、有理数まで拡張された指数について、正しく意味を理解して計算できるようにすること
指数関数のグラフ・方程式・不等式の扱いに慣れること
という2つの大きなステップがあるので、これに沿って進めていくのが良いでしょう。
どちらのステップにおいても、ある程度パターンは決まっている単元なので、得意にするためには演習の量が大切になります。そのため、基本的には学校で配布される4STEPなどの傍用問題集や、チャート式などの網羅的な問題集といった、問題数の多い参考書に取り組むのがおすすめです。
また、模試や入試で実際に出題される場合には、他の単元との融合問題も多いため、基礎知識を身につけた後は、知識を整理しながら進められる解説の詳しい参考書を用いるのがオススメです。
ここでは、指数関数の演習量を確保しつつ、理解を深めるのにピッタリな参考書・問題集をいくつかご紹介しますので、参考書を買う際の参考になれば幸いです。
※ 共通テストを始めとして、指数関数は対数関数とともに出題されることも多く、内容としても深いつながりを持つため、対数関数とともにマスターしていくのがおすすめです!
苦手な方向け

単元のピンポイントな学習に最適な、数学Ⅱの指数・対数分野に特化した参考書です。基礎から丁寧に解説されているので、苦手な方や、学校の授業について行けなくなってしまって復習したい方に向いています。
タイトルは「指数・対数」ですが、それぞれ、指数関数、対数関数までカバーされています。

この参考書は、問題演習のみならず、各単元の導入から詳しく解説されているのが大きなおすすめポイントです。各単元の内容を理解した上で、取り組みやすい問題かつわかりやすい解説で知識を定着させていけるので、先取り学習や、弱点克服にとても役に立ちます。
数学2Bの他の単元も含まれますが、指数関数・対数関数だけ取り組む、といったピンポイントな使い方もおすすめです。
公式を覚えて次のレベルに進みたい人向け

公式は覚えたし、教科書的な知識はあるのに、いざ模試などのテストになると三角関数が解けない方にとてもオススメの参考書です。厳選された良問を通じて、問題を解く上でのポイントを学べます。問題数もそこまで多くないので、指数関数・対数関数だけ数日でガッと強化する、といった使い方も可能です。
難関大レベルまで実力を伸ばしたい方向け


理系数学の良問プラチカ 数学ⅠAⅡBC (河合塾シリーズ 入試精選問題集 5)(大石隆司、河合出版) / 文系数学の良問プラチカ 数学ⅠAⅡBC(河合塾シリーズ 入試精選問題集 4)(鳥山昌純、河合出版)
応用レベルの頻出テーマが必要最小限の問題で網羅されており、解説も詳しいので、得点源にしたい場合には、これらの中の「指数関数・対数関数」の範囲の問題を解いていくと効率が良いです。記述模試や実際の入試問題でよく見かけるテーマが凝縮されているので、模試になると解けなくなる方などにもおすすめです。
※「理系数学のプラチカ」よりも、「文系数学のプラチカ」の方が難しいので、注意してください。最難関大を目指す方以外は、文系の方であっても「理系数学の良問プラチカ」を使うのがおすすめです!
演習量を増やし、知識を確実に定着させるならDr.okke
指数の拡張や指数関数の分野では、定義・公式の定着や、問題のパターンへの慣れがとても重要ですが、参考書では、すぐに下のポイントから必要な知識が見えてしまったり、一度解いてしまうと「ここのページはこの解法だな…」と、問題の場所から公式や解法が推測できてしまったり、そもそも問題の解答を覚えてしまったりと、定着度の確認や効果的な反復演習を行うことが難しい場合も多いです。
そこで新しいテスト作成ツールであるDr.okkeをご紹介いたします。
いつでもすぐにテストを作成・実施
教科書の内容確認レベルの基礎から大学入試レベルの応用問題までを網羅しており、今日の授業でやったテーマに絞ったチェックテストから、分野を混ぜた実力テストまで、全て1分で簡単に作成可能です。
計算の一行問題に特化した「計算ドリル」という科目も別で用意しており、指数の拡張や指数関数について、定義・公式の運用や計算力をとにかく鍛えるといった使い方も可能です。
充実した良問とシャッフル出題によって、指数の拡張・指数関数のそれぞれの公式や知識を定着させられているかを確実にチェックできます。定義や公式の知識の定着が重要になるこの単元の力を引き上げるには、まさにピッタリのツールです。
※ 難易度調整、制限時間設定も簡単にできます。また、基礎的な一行問題で反復演習ができる「計算ドリル」の科目も別途用意しております。
自動採点かつ、受験結果のデータが蓄積
テストを受けた直後に結果が表示され、解説も手作りでかなり詳しく作っているため、疑問を残さず、理解も深められます。
受験結果がデータとして自動で蓄積されるので、生徒さんの理解度や今復習すべき単元などが一目で分かります。これからのカリキュラムや学習計画を立てる際に、より一人ひとりに寄り添った指導を実現することができます。
無料体験期間もありますので、ぜひ一度お試しください。

Dr.okkeの導入をご検討の方は、こちらの画像をタップし、無料トライアルをお試しください!確認テストはDr.okkeにおまかせください!
まとめ
この記事では、指数関数(指数の拡張・指数関数・グラフ)の単元で出てくる定義や公式を、思い出し方を含めて総まとめするとともに、おすすめ参考書を紹介しました。あまりボリュームは多くない単元ですが、新しい定義がたくさん出てきますので、慣れていかないと問題を解くことが難しく、苦手な方にとってはハードルの高い単元です。
どの単元でも同じですが、学習の際にとても大切になるのは、定義や公式を忘れてもすぐに思い出せるよう、普段の演習のときから「自力で思い出すクセ」をつけておくことと、自分の理解度に合った解説の詳しい参考書を選び、内容をしっかり理解した上で押さえていくことです。毎回教科書の定義や公式を見ながら問題を解いていては、いつまで経っても自力で思い出すことはできません。
また、使う式がわかって方針を立てられても、計算力が無いと正答できないため、普段の演習から最後まで自分の手で計算するようにすることが重要です。
上で紹介したように、解説の詳しい市販の参考書や問題集もたくさんありますが、問題の並びで使う公式や解法が推測できてしまったり、最後まで解き切らず、解法だけ合っていたら先に進んでしまったりと、どうしても効果的な学習ができないこともあります。その際には、Dr.okkeのようなテストツールを有効活用し、定着させられているかを確認しながら着実に学習を進めていくことが、指数関数の得点アップへの近道となるでしょう。(もしDr.okkeにご興味がありましたら、こちらまでご連絡ください。無料トライアル実施中です!)
指数関数は、教科書でのページ数が少ない割に、新しい定義が登場して手強い単元ですが、模試や受験でも頻出ですし、理系の方は数学Ⅲでもたくさん登場するテーマであるため、ぜひ得意にしておきたい単元です。また、量が少ない分、短期間で仕上げることも可能です。この記事を参考に苦手意識を克服し、試験本番で確実に解けるように効果的に学習に励んでいきましょう。
執筆者
株式会社okke代表。ラ・サール中高、東京大学工学部計数工学科卒。
財務省に勤務したのち、アメリカ・UCLAでMBAを取得し、能動的に学ぶ人を社会に増やすべく、okkeを起業。
Dr.okkeのコンテンツを作っています。

