はじめに

高校生に数学を教えていると、多くの生徒が数学に苦手意識を持っていることに気付かされます。中でも数学Bの「数列」に苦手意識のある方は多いのではないでしょうか。数列はそもそも学ぶ量が多いうえに、シグマという複雑な記号、知らないと解けない解法パターン、他の単元とのさまざまな融合問題などが登場してくる点で、生徒さんたちの「できない」という感覚を増幅させているように見えます。

実際に、問題集を買って一度覚えた気になっても、いざ模試やテストで出題されると解けないことが多いのも事実です。さまざまな方々が数列を難しい単元の一つに挙げています。

参考：高校数学難しい単元５選。でも難しそうで慣れると実はそうでもない単元もある、【高校数学】各単元分野別　難易度・重要度

とはいえ、入試では、数列は共通テストや二次試験いずれにおいても頻出分野ですし、新課程ではベクトルが数Cに移行した分、（「数学ⅡB＋ベクトル」のように扱われることが多いので依然としてベクトルも重要ですが）数Bにおける数列の占める割合が上がっています。

そこで今回は、数列の全体像や勉強法、苦手な方が多い漸化式の基本的な解き方、おすすめの参考書などについてまとめて解説してみましたので、ぜひ最後まで読んでみてください。

数列の主なパターン

数列の分野は、まずはさまざまな解法のパターンを理解し、自分の手で解けるようになるまで繰り返し解いて定着させ、その後、目の前の問題がどのパターンで解けるかを正確に判断する練習をすることが得点力アップにつながります。

数列においては、まずは基本的な数列である「等差数列、等比数列」の一般項と総和の求め方をその理由を含めてマスターしましょう。話はここからです。

そして、次にシグマの計算です。形は複雑ですが、やっていることは単純なので、意味を理解しながら公式を使いこなせるようになりましょう。部分分数分解や、等差数列×等比数列の形の数列の和の計算など、知っていないと厳しいパターンも多いので、ある程度解き方も暗記していきましょう。

ここで、中ボスとして群数列が登場します。思考力が問われるテーマですが、群の中の話なのか、全体の話なのか、しっかりと頭を整理していくことで解きやすくなります。

そして漸化式が登場します。苦手な方も多いと思いますが、一般項が求められるパターンはある程度決まっています。まずは基本的な形である「等差数列型、等比数列型、階差数列型」をマスターし、その後、特性方程式を利用した「二項間漸化式、三項間漸化式」を解けるようになりましょう。ぜひ、なぜそれで一般項が求められるのかという理由を理解するようにしてください。分数型や累乗型、また対数をとるパターンなど、他にもいろいろと頻出パターンがあるので、たくさんの問題に触れて、慣れていくことが重要です。

最後に、数学的帰納法というテーマも登場します。これは入試でも証明問題の便利なツールとして大活躍するので、必ず自分で手を動かして答案を書きながら、使えるようにしておきましょう。

このように、数列では解法パターンの理解と定着がとても大事ですが、実際の共通テストでは、数列は長文問題として出題されることが多く、読解力や計算力も求められます。

例えば、令和4年度（2022）はこのような数列の問題が出題されました。やっていることがわかれば、簡単な漸化式の問題なのですが、文章が長く、内容を正確に読み解いていく必要があります。

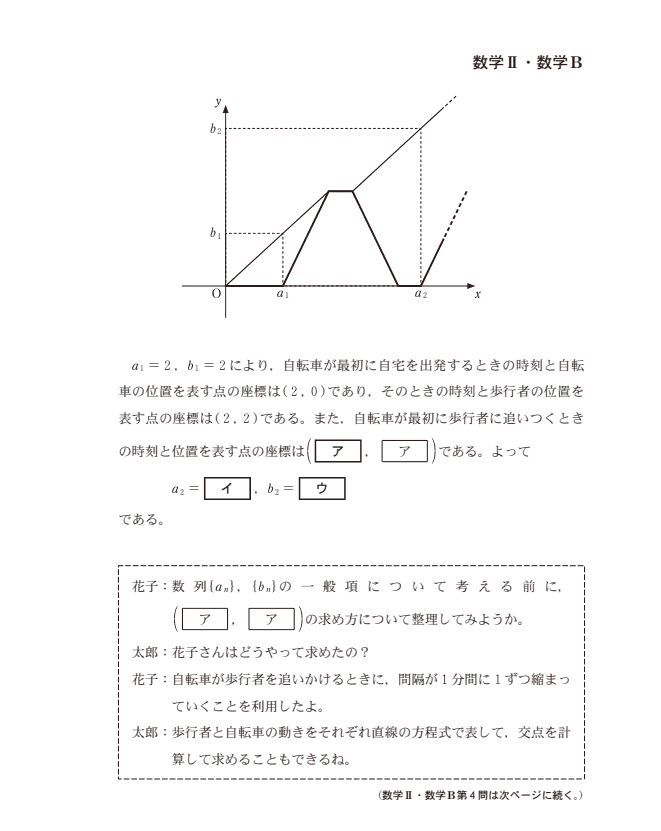
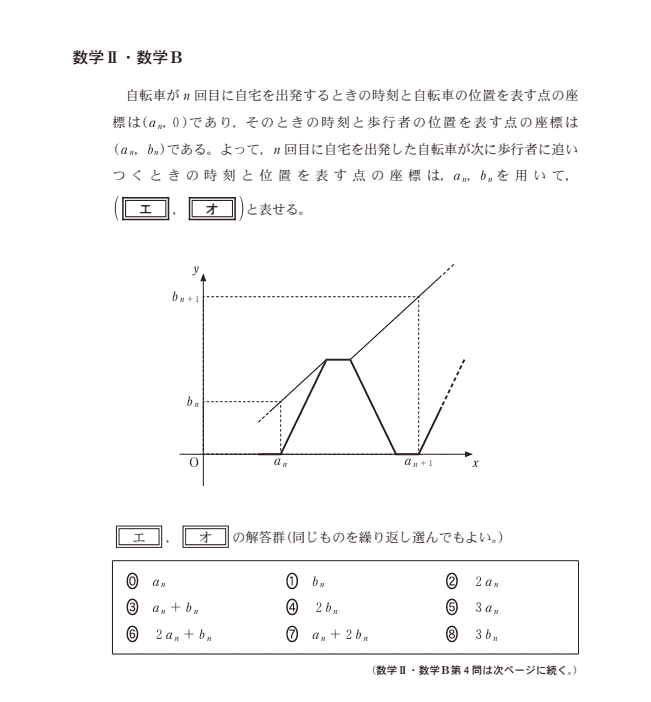
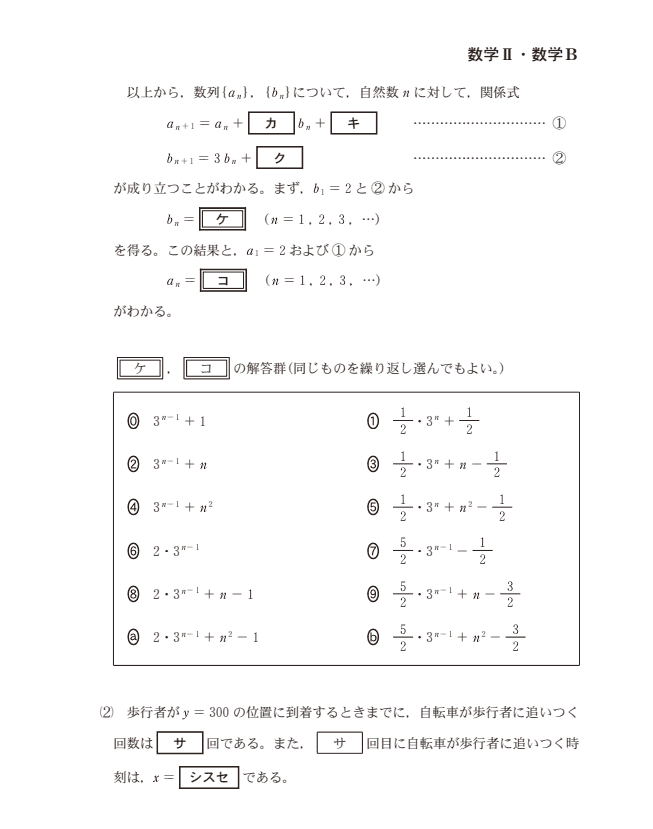
出典：大学入学共通テスト　令和4年度　本試験　数学Ⅱ・数学B

このように問題文が長い場合には、初めて出会う問題の設定を正確に読み解いていく力が求められます。その力は一朝一夕には伸ばせないので、とりあえず知っている問題に行き着いた後に、正確に素早く解けるように、日頃から時間を測りながら、さまざまな解法パターンを演習しておきましょう。

では、参考までに、上で挙げた漸化式の代表的な5パターンの解き方をざっと紹介します。

解法①「等差数列型」

→ 詳しくは、こちらで確認しましょう。

解法②「等比数列型」

→ 詳しくは、こちらで確認しましょう。

解法③「階差数列型」

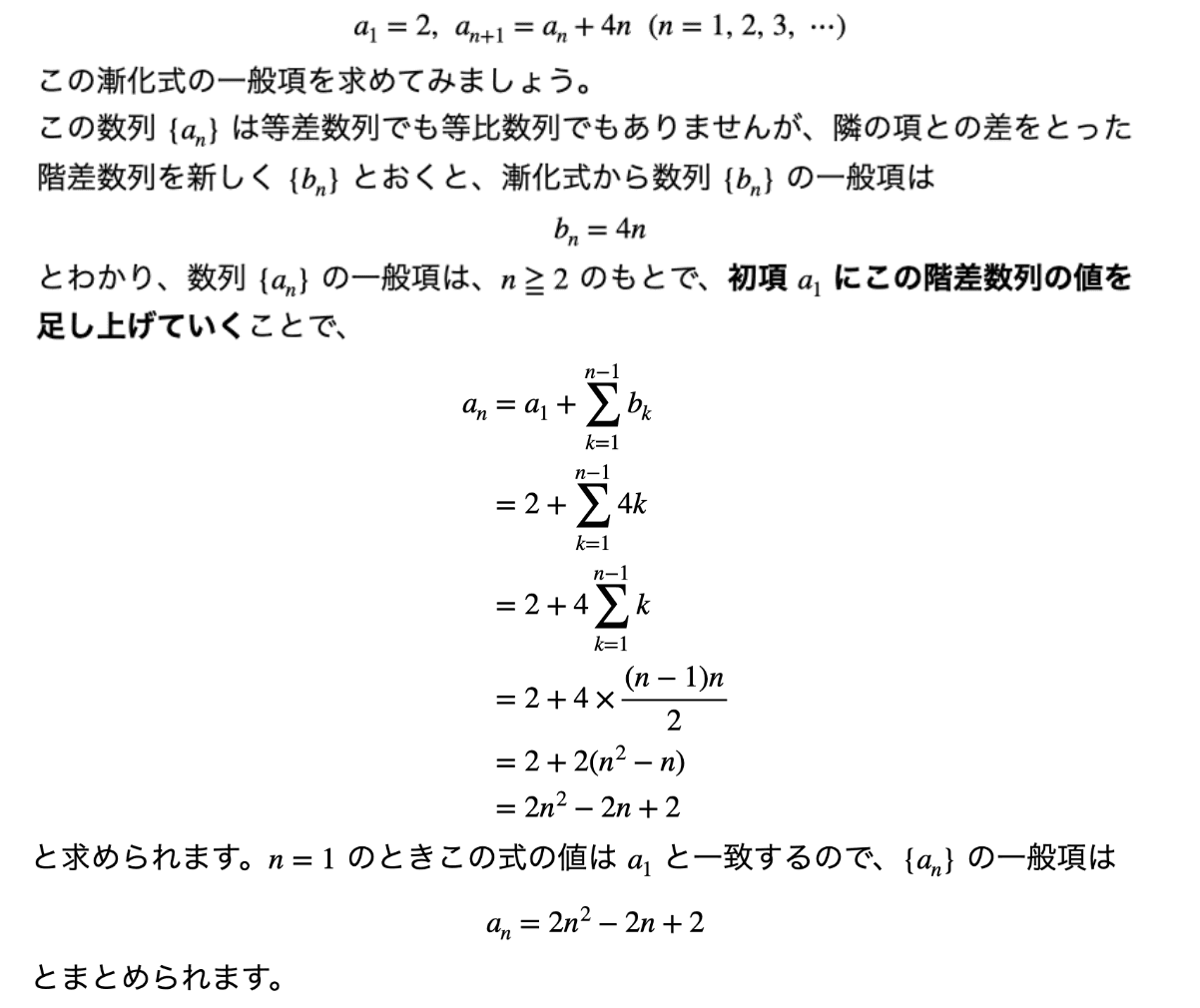
→ なぜn≧2で場合分けしないといけないのかなど、詳しい背景はこちらで確認しましょう。

解法④「二項間漸化式」

→ （※）の方程式を特性方程式と呼ぶことがあります。このパターンの二項間漸化式では、「なぜこの方程式の解を使うと、うまいこと一般項が求められる形に変形できるのか」を理解することがとても大事です。実はこの特性方程式というのは、そもそも一般項を求めるため「等比数列に変形したい」という目的で作られたものなのです。詳しい背景はこちらで確認しましょう。

解法⑤「三項間漸化式」

→ （※）の方程式も特性方程式と呼ぶことがあります。④で紹介した二項間漸化式と同様、「なぜこの方程式の解を使うと、うまいこと一般項が求められる形に変形できるのか」を理解することがとても大事です。この特性方程式も、そもそも一般項を求めるため「等比数列に変形したい」という目的で作られたものなのです。詳しい背景はこちらで確認しましょう。

以上、①〜⑤のパターンの漸化式については特に、考えなくても勝手に手が動くようになるくらいまで練習しておきましょう。その上で、分数型や累乗型、また対数をとるパターンなど、他の頻出パターンの問題にも触れて、解法の引き出しを増やしていきましょう。

おすすめの参考書

数列は出題パターンがさまざまなので、自力で解けるようになるためには、それなりの演習量をこなす必要があります。基本的には学校で配布される問題集などを用いるだけでも十分ではありますが、ここでは数列の理解を深め、演習量を確保するのにピッタリな参考書・問題集をいくつかご紹介します。

教育課程の変更によって単元の移行があったとはいえ、数列に関しては特に内容は変わっていません。これまでに出版されてきた多くの参考書の中から、自分に最もフィットするものを選ぶようにしましょう。

まず、弱点克服に最適な、数列に特化した参考書・問題集です。

・「改訂版 坂田アキラの数列が面白いほどわかる」（坂田アキラ、KADOKAWA出版）：基礎的な内容から入試標準レベルまでを網羅しているため、数列に苦手意識を持っている方におすすめの一冊です。

・「教科書だけでは足りない大学入試攻略数列」（河合塾series）（鈴木克昌、河合出版）：問題量が豊富で、幅広い出題形式を扱っているので、教科書や学校の問題集だけでは演習量が不足していると感じる場合に最適です。

以下は、他の分野も含んでいる参考書・問題集になります。

・「文系数学の良問プラチカ 数学ⅠAⅡB」 (河合塾シリーズ 入試精選問題集 4)（鳥山昌純、河合出版）および「理系数学の良問プラチカ 数学ⅠAⅡB」(河合塾シリーズ 入試精選問題集 5)（大石隆司、河合出版）：応用レベルの頻出テーマが必要最小限の問題で網羅されており、解説も詳しいので、数列を得点源にしたい場合には、これらの中の「数列」の問題を解いていくと効率が良いです。記述模試や実際の入試問題でよく見かけるテーマが凝縮されているので、模試や過去問になると解けなくなる方などにもおすすめです。

※「理系数学の良問プラチカ 数学ⅠAⅡB」よりも、「文系数学の良問プラチカ 数学ⅠAⅡB」の方が難しいので、注意してください。最難関大を目指す方以外は、文系の方であっても「理系数学の良問プラチカ」を使うのがおすすめです。

数列の学習において最も重要なのは、様々な解法のパターンを身につけ、自力で解けるようになるまで定着させることです。そのためには、十分な量の演習が不可欠となります。ここで紹介した参考書を有効活用することで、数列の理解を深め、得点力を着実に高めていくことができるでしょう。

単なる暗記にとどまらず、なぜその解き方でうまくいくのか、を地道にしっかりと考えるようにしていきましょう。これが、共通テストや二次試験の応用問題の対策につながります。

現状を知り、演習量を増やすならDr.okke

何度も述べていることですが、数列は量も多いため、基礎的な内容から入試レベルまで、自分がしっかり身につけられているかを確認することはとても難しいです。そこで、簡単にテストが作成でき、現状を客観的に知ることのできるツール「Dr.okke」をご紹介します。

1. いつでもすぐにテストを作成・実施

• 「シグマ」「漸化式」といった小単元や、「基礎」「応用」のレベルに分かれており、どんなテストでも1分で作成可能です。（単元やレベルを混ぜて出題することも可能です）

• 必要最小限の問題で数列の必要な知識が網羅されており、また、シャッフル出題もできるので、自分が数列の知識をしっかりと身につけられているかを確かめられます。（参考書や問題集では、意識しなくても、並びなどから使う公式がわかってしまうことも多いです）

もちろん他の単元や科目も充実しています！

2. 自動採点かつ、受験結果のデータが蓄積

• テストを受けた直後に結果が表示され、それぞれの問題に、手書きの図や別解なども含めた詳しい解説も付いているため、理解を深められます。

• 客観的なデータが自動で蓄積されていき、復習すべき単元などが一目で分かるので、学習計画も立てやすくなります。解けていない問題のみでの出題も可能です。

無料体験期間もありますので、ぜひ一度お試しください！

まとめ

冒頭にも述べた通り、数列は、シグマという複雑な記号が出てきたり、知らないと解けない解法パターンが多かったりと、高校数学の中でも特に苦手意識の生まれやすい分野です。一度苦手意識を持ってしまうと、その克服は容易ではありません。しかし、数列は、パターンを攻略できれば得点源となる問題も多く、共通テストや大学入試においても頻出の単元であるため、得意分野にしていきたいものです。

そのためには、理解を深めながら地道に定着させていくことが重要です。本記事で紹介した参考書やDr.okkeといったツールを有効活用し、自分が定着させられているかを確認しながら着実に学習を進めていくことが、数列の得点アップへの近道となるでしょう。

数列に苦手意識を持っている方も、ぜひ本記事で紹介した参考書やツールを試してみてください。そして、自分なりの学習方法を確立し、ぜひ数列を得意分野の一つに加えていってください。困難な道のりかもしれませんが、努力を重ねることで必ず結果はついてくる単元です。数列を克服し、入試本番で高得点を取れるよう学習に励んでいきましょう。