弧度法とは

三角関数の話に入る前に、まずは大事な「弧度法」という「角度の測り方」をつかんでおきましょう。

分度器で測るような 30° や 60° などの角度は、いわゆる「度数法」の角度と呼ばれます。度数法では、円周を 360 等分した弧の、中心に対する角度を「1°」と定義していました。（1 周が 360° であることを考えるとわかりやすいですね）

これに対し、円の半径に等しい長さの弧の中心に対する角度を 1 ラジアンと定義し、弧の長さを半径の長さで割ったものを、その中心角の角度として測っていく方法を「弧度法（ラジアン）」と呼びます。（1 [rad] とも書きます。rad はラジアンの略です）

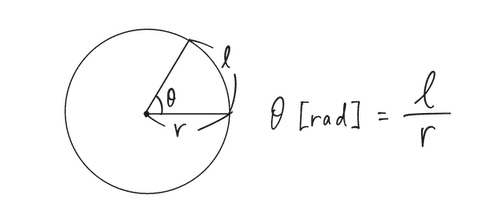
「°」（度）とラジアン（rad）の単位間の関係も大事です。中心角が 180° や 360° の孤を考えてみましょう。中心が r の円で考えると、定義から

• 中心角が 180° のとき、孤の長さは πr となるので、中心角を弧度法で測ると πr / r = π [rad]

• 中心角が 360° のとき、孤の長さは 2πr となるので、中心角を弧度法で測ると 2πr / r = 2π [rad]

となります。つまり、

• 180° = π [rad]

• 360° = 2π [rad]

であることがわかります（同じ角度を、どう測って表しているかの違いです！）。これはいつでも思い出せるように、理由も合わせて絶対に押さえておきましょう。

三角関数の定義（単位円を考える）

数学Ⅰでは、直角三角形による三角比の定義を学びましたが、それでは0°〜90°しか考えることができないため、ここではより広い角度で定義できる方法を考えていきます。

それが単位円（半径が1の円）を用いた考え方です。x軸正の向きから測った角度 θ（時計回りを正、反時計回りを負とします）が決まると、それに対応する単位円上の点が1つに決まるので、その点に対して、

• y座標を sinθ

• x座標を cosθ

• 動径の傾きを tanθ

と定めます。（動径とは、単位円の中心から、その点の方向へ伸びる半直線のこと）

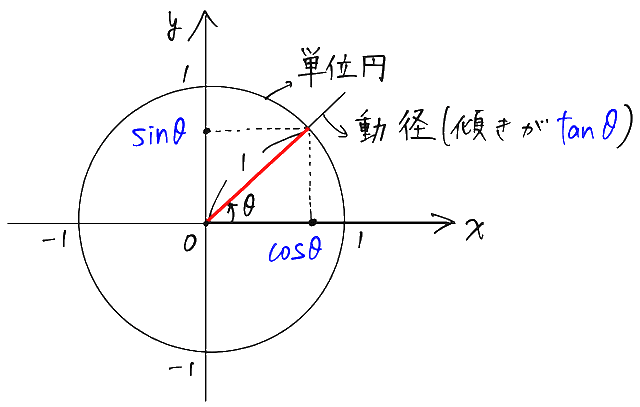
ちなみに、単位円の半径は 1 なので、このように定義しても、0°〜90° の場合は直角三角形による三角比の定義と同じになることを確認しておきましょう！これを知っておくと、「sin は y 座標だっけ？x 座標だっけ？」とわからなくなったときに思い出しやすくなります。

この一般的な定義によって、全ての実数 θ に対してsin, cos, tanの値を定義できるようになり、そのような関数のことを「三角関数」と呼ぶのです。

三角関数の公式を一気にマスター！

では、三角関数の公式を一気にマスターしていきましょう。最初のうちは、「自力で」毎回頭の中や紙の上で式を導出し、使っていくうちに自然と覚えるようにしましょう。そうすると、「公式覚えてるかな...？」と不安になることも無くなります。

毎回教科書の公式を見ながら問題を解いていては、いつまで経っても公式を身につけることはできないので注意しましょう！！

90°（π/2）や180°（π）の公式

ではまずは、90°（π/2）や180°（π）についての公式をマスターしていきましょう。たくさん式が登場しますが、これも上の単位円の定義をわかっていれば全てすぐに思い出せます。

−θの式

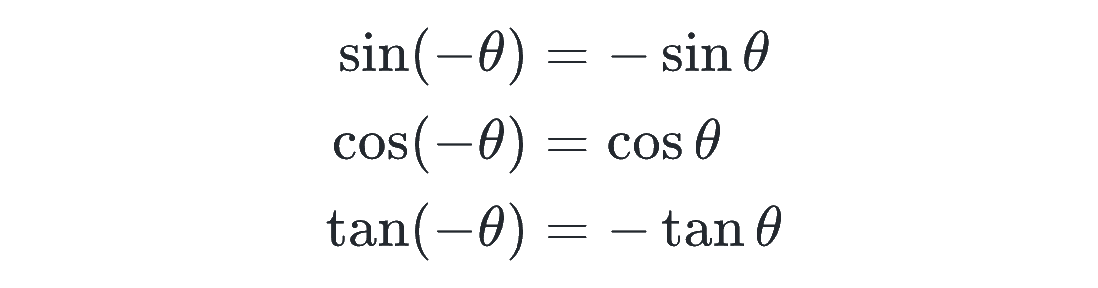
これは、単位円で、θ に対応する点と、−θに対応する点が、下のグラフの通りx軸に関して対称になっていることからわかります。

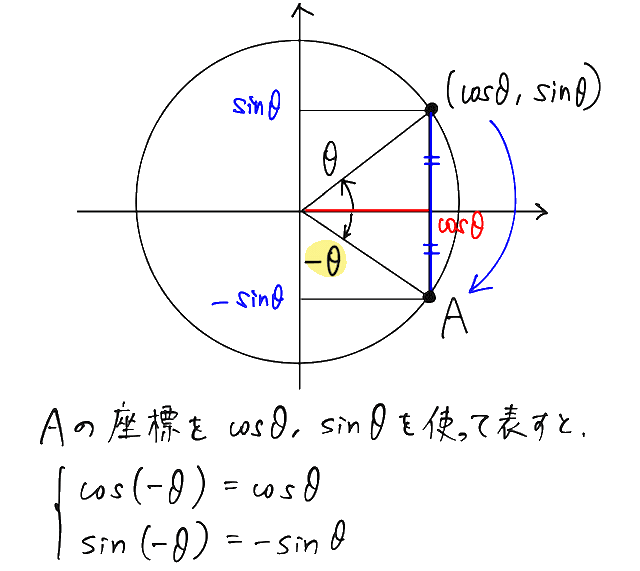
90°（π/2）関係の式

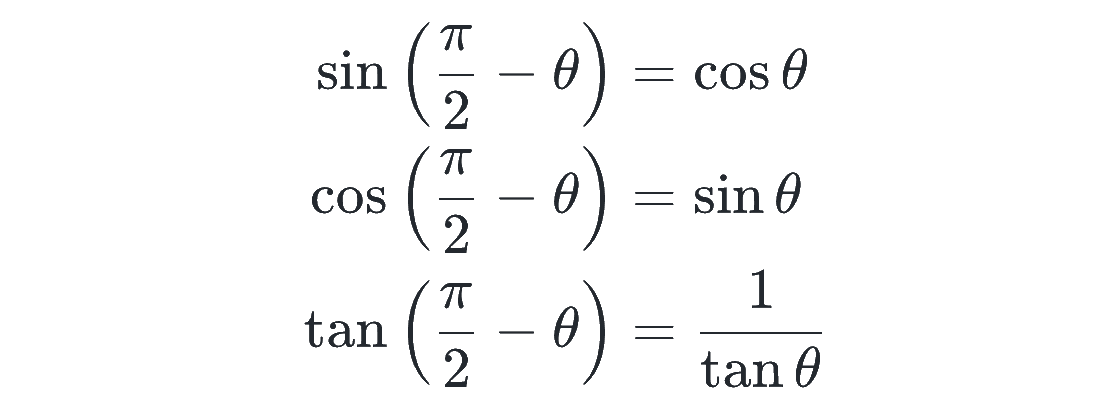
まずは、π/2 [rad] = 90° であることを思い出しましょう。

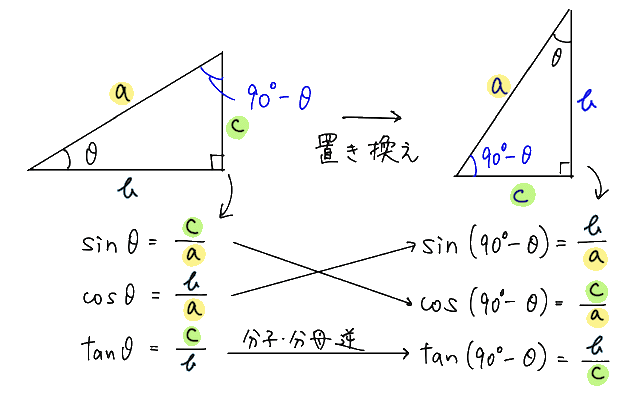
これは、単位円で考えても良いですが、思い出す上では、直角三角形による三角比の定義の方がわかりやすいです。

続いてはプラスバージョンです。

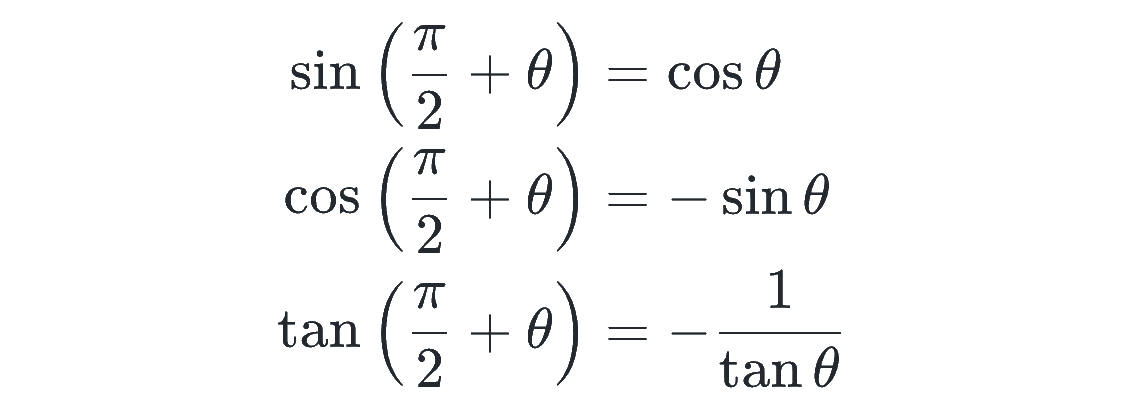
これは以下のように単位円で考えるとすぐに思い出せます。

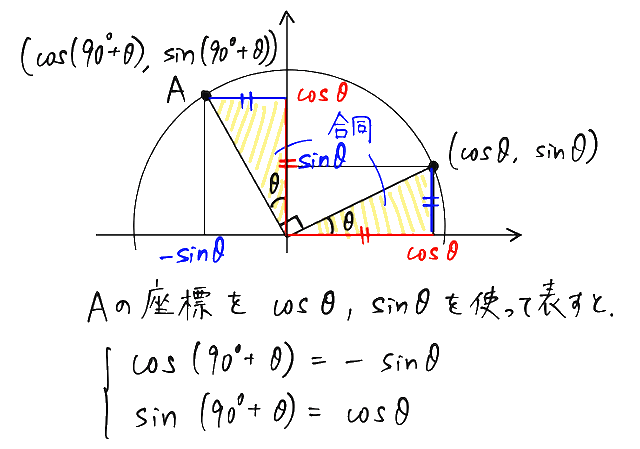
180°（π）関係の式

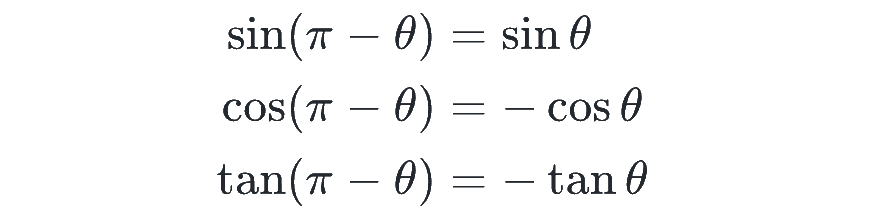
これは以下のように単位円で考えるとすぐに思い出せます。π [rad] = 180° であることを思い出しましょう。

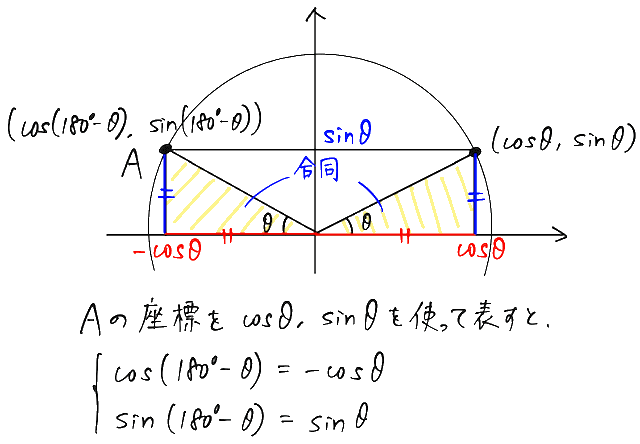
このように、単位円で何を表しているかを把握すれば、例えば sin(270°-θ) のようによくわからない式が出てきたときにも対応できるので、最初は大変でも毎回単位円から導くようにしましょう！（下で学ぶ加法定理を使って思い出すのもおすすめです）

三角関数の相互関係

では次に、相互関係の式について。これは、三角比で学んだものが、そのまま成り立つので、さらっと紹介します。

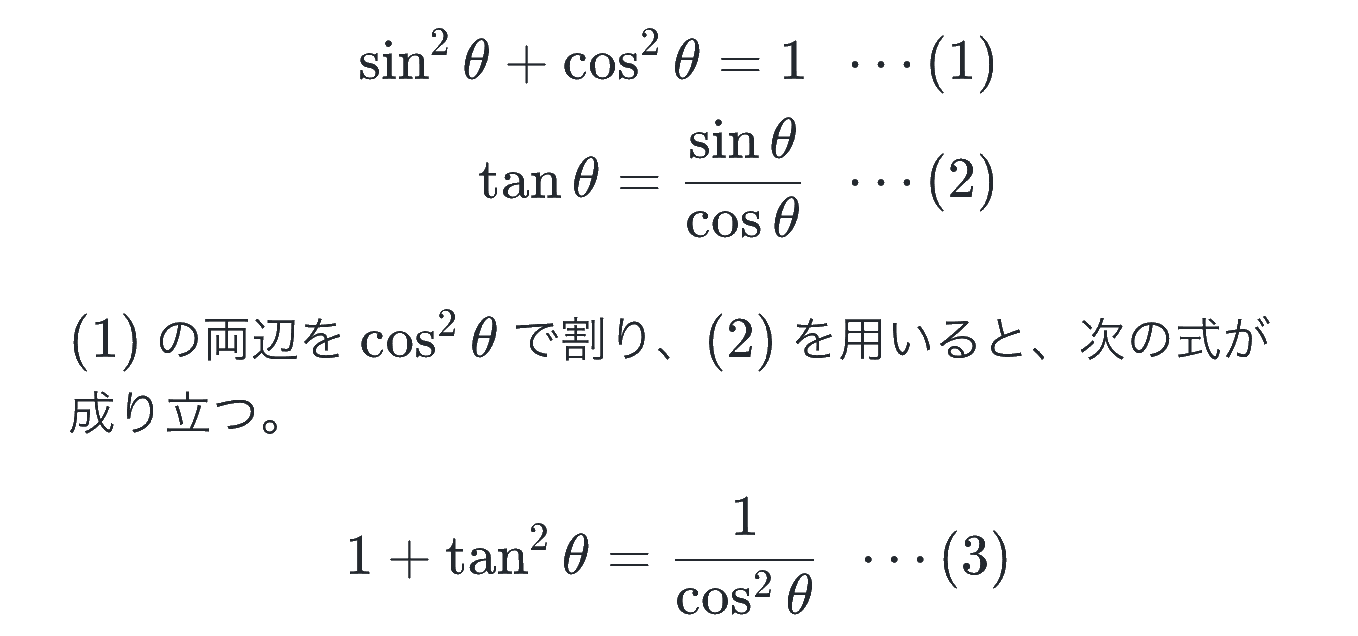
使い方が重要で、これらの式を自在に使いこなせるようになりましょう。

• (1)式は sin と cos の関係式で、どちらかを知りたいときにもう片方から求めることができる

• (2)式は sin と cos から tan を求めるという使い方が多い

• (3)式はcos と tan の関係式で、どちらかを知りたいときにもう片方から求めることができる

では加法定理に入る前に、まずはここまで学んだ基本知識の復習として、問題を解いてみましょう！（答えがすぐ下にあるので注意）

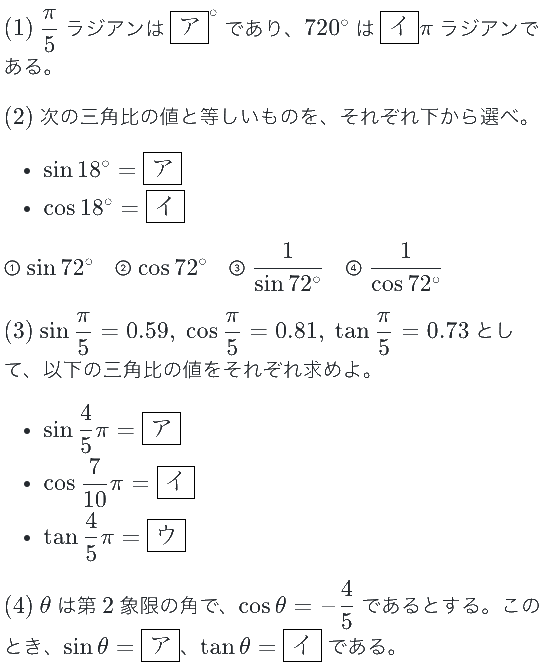
※弊社サービスのチェックテスト作成ツール「Dr.okke」より引用。このようなチェックテストが1分で作れます。

答：(1) 36・4 (2) 2・1 (3) 0.59・-0.59・-0.73 (4) 3/5・-3/4

加法定理

では加法定理について。この下で出てくる公式は、全てこの加法定理から導いていくので、これらの式は確実に押さえておく必要があります。

まずはこの4つの基本式。

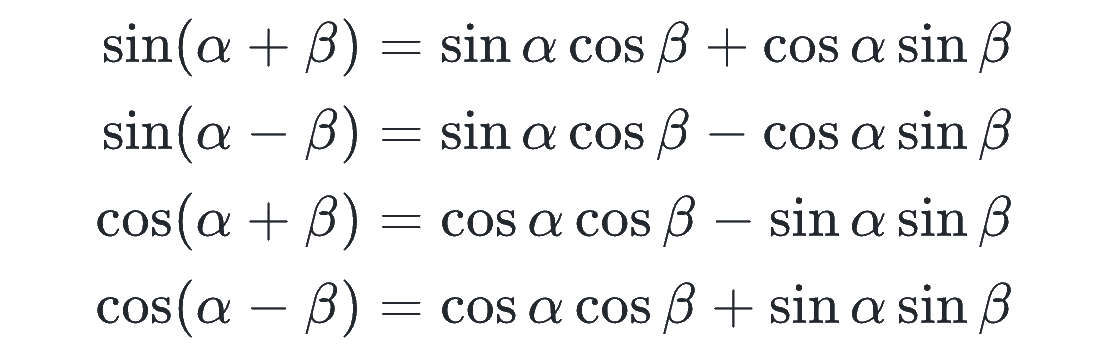
証明についてはここでは省略するので、例えばこのokke用語のページを見て確認しておきましょう。（加法定理の証明は、東京大学の入試問題で出題されたことでも有名です）

これらを用いると、tan の加法定理を作ることができます。

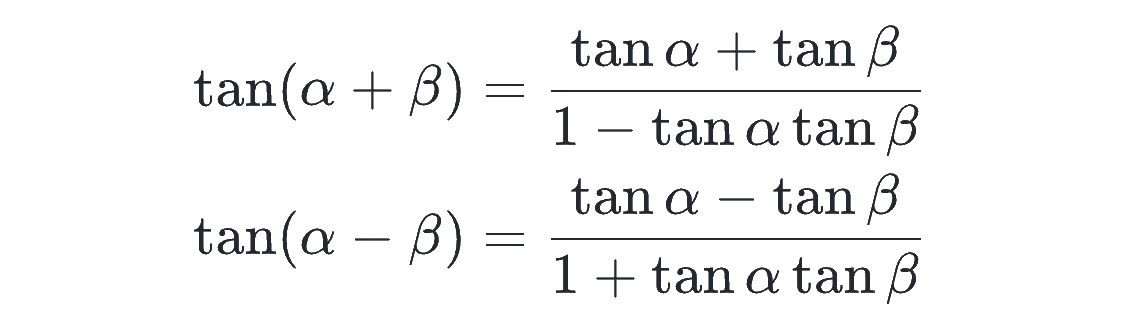
これは覚えてなくても、その都度導ければOKで、上で解説した相互関係の(2)式（tan = sin / cos）を用いつつ、分母分子を cosα cosβ で割るのがポイントです！

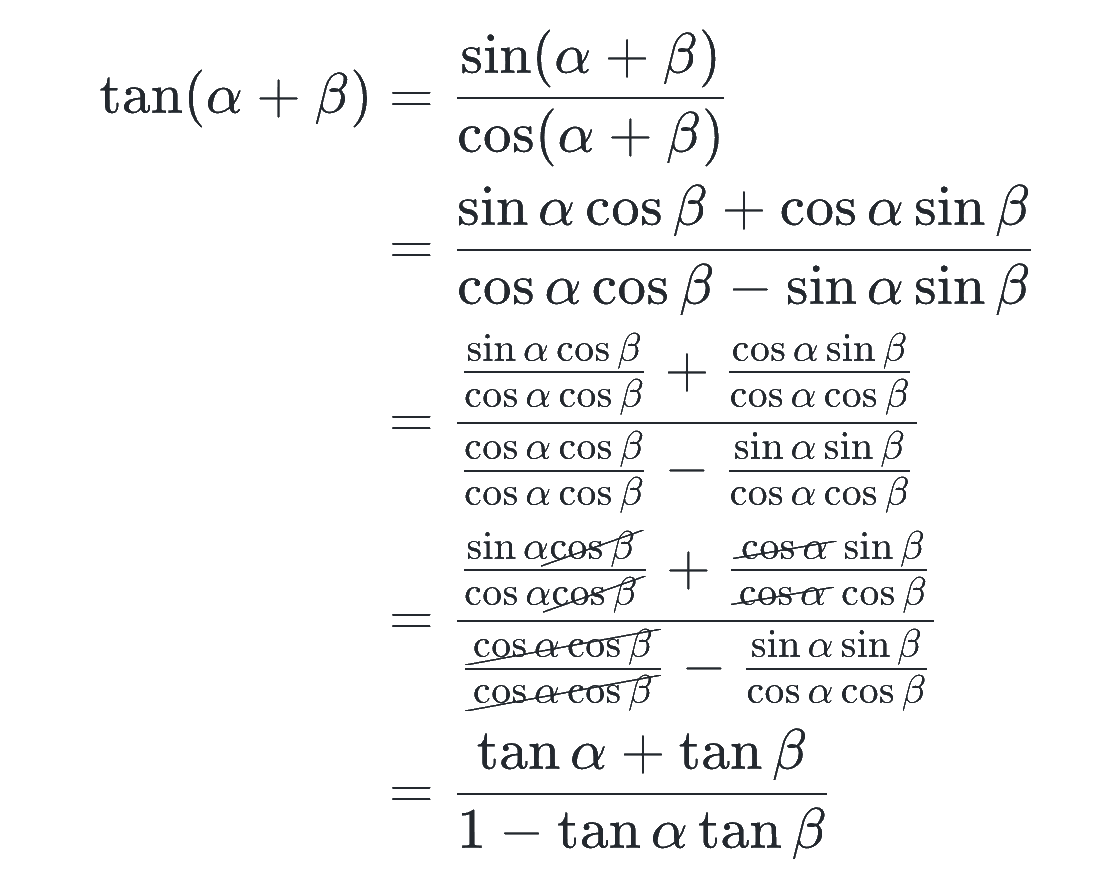
マイナスの方も同様に示すことができるので各自やってみましょう。

では、問題を解きながら、加法定理の知識を定着させましょう。（答えがすぐ下にあるので注意）

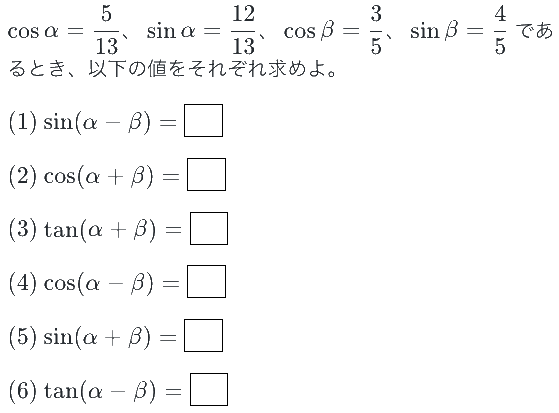
※弊社サービスのチェックテスト作成ツール「Dr.okke」より引用。1分で楽に、このようなチェックテストが作れます。

答：(1) 16/65 (2) -33/65 (3) -56/33 (4) 63/65 (5) 56/65 (6) 16/63

2倍角の公式

sin と cos の加法定理を用いると、次の2倍角の公式を導くことができます。

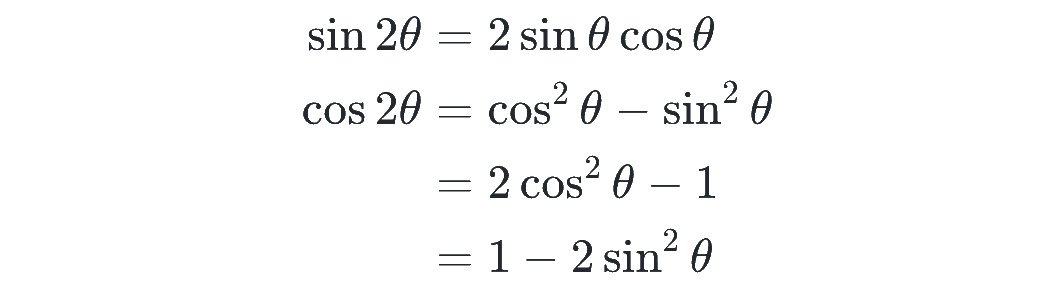
2θ（2倍角）をθで表せるのがこの公式のポイントです！

cos の方は3つのパターンがありますが、cos だけで表した2つ目の式、sin だけで表した3つ目の式をよく使います。場面に応じて使い分けられるようにしましょう。

これらの式は、いつでも加法定理から作れるようにしておきましょう！

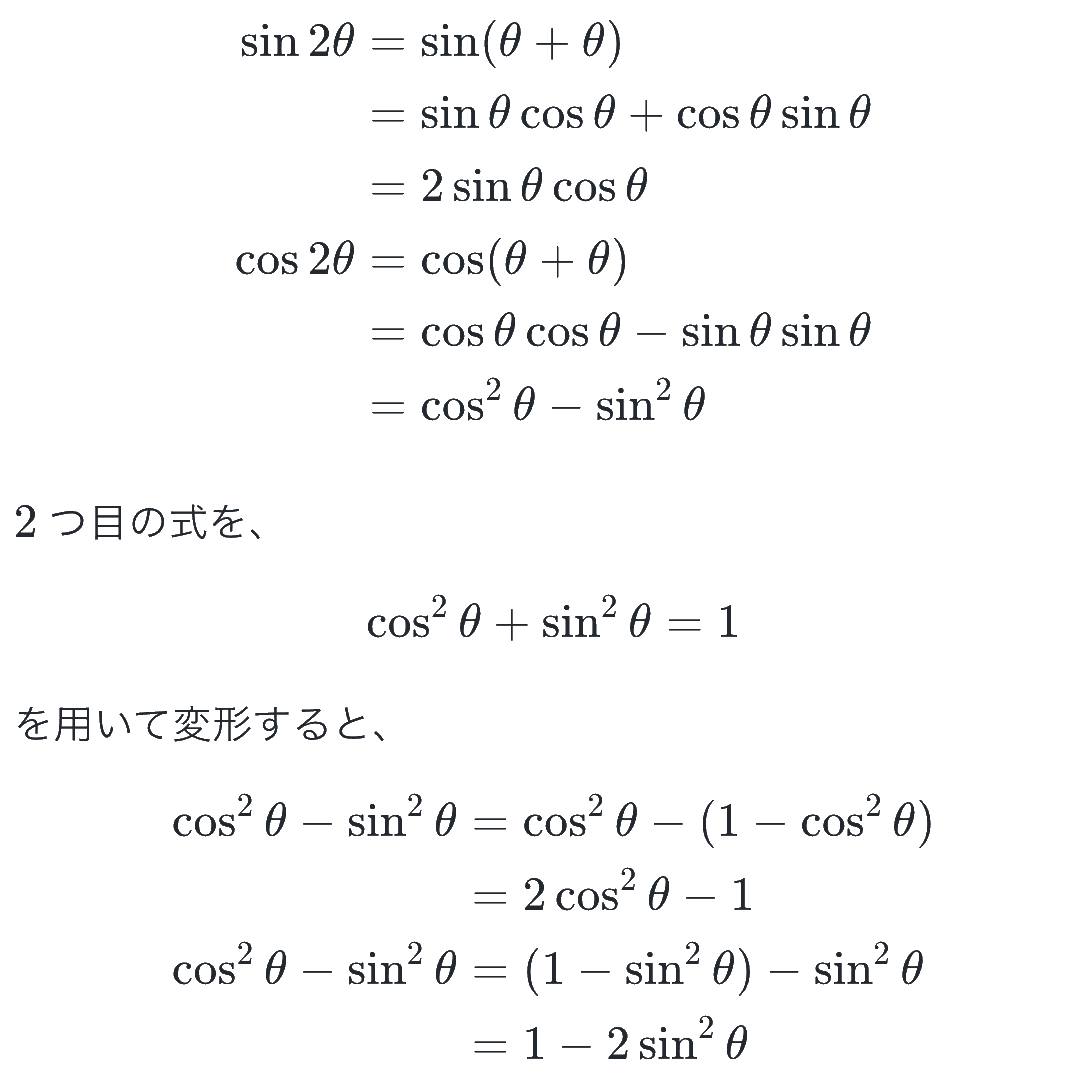
さらに、tan の加法定理を用いると、tan の2倍角の公式も導けます。

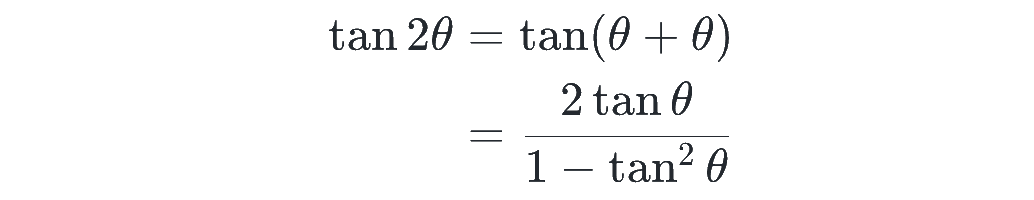
半角の公式

cos の2倍角の公式の、2つ目と3つ目の式を変形すると、半角の公式を導くことができます。これは、要するに2倍角の公式の主役を変えたような式です。

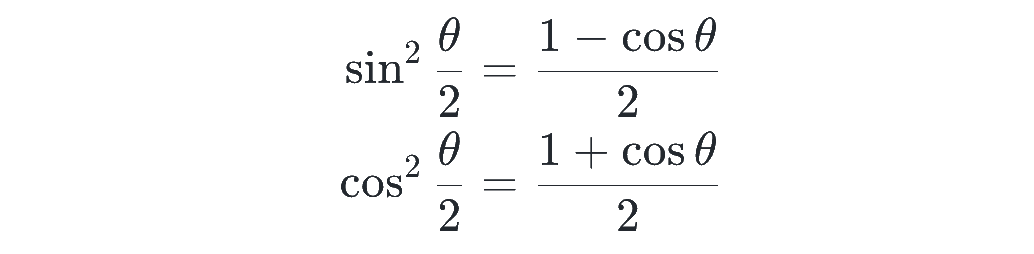
導出としては、2倍角の公式の θ を θ/2 に変えて、

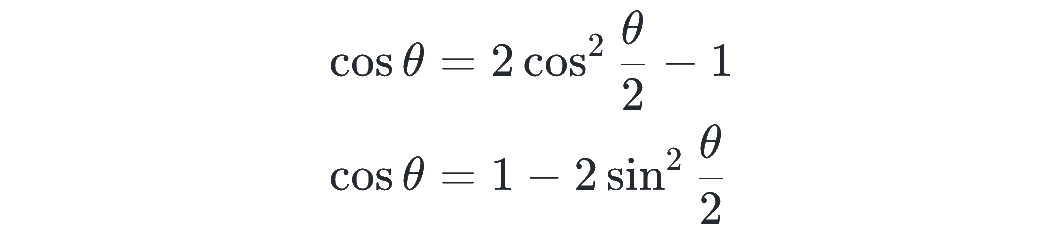
が成り立つので、これをそれぞれ変形すれば、

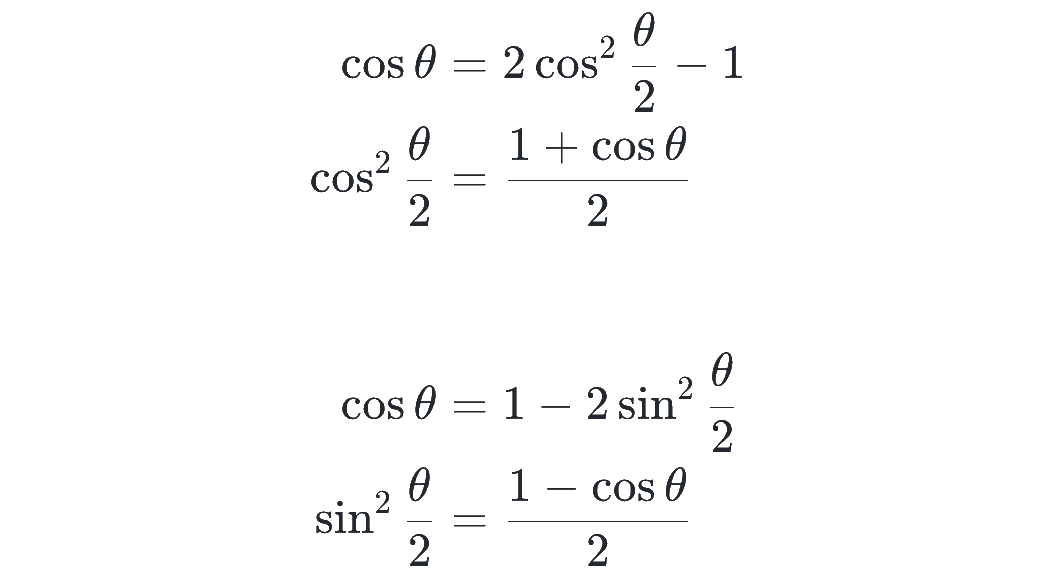
と示されます。

3倍角の公式

2倍角の公式や加法定理を組み合わせると、次の3倍角の公式が成り立ちます。

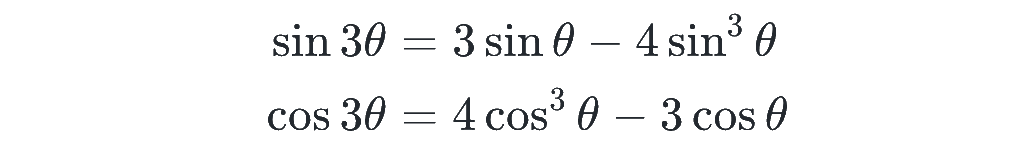
見た目の通り、3θ（3倍角）をθで表せるのがこの公式のポイントです！左辺と右辺で sin と cos がそろっていることにも注目しておきましょう。

導けたら覚えておく必要は無いですが、そこそこよく登場するので、解くうちに覚えていくのが理想です。

いずれにせよ、3倍角の公式の導出では、いろんな公式が登場して復習になるので、いつでも導けるようにはしておきましょう！とにかく sinθ や cosθ にどんどん置き換えていくのがコツです。

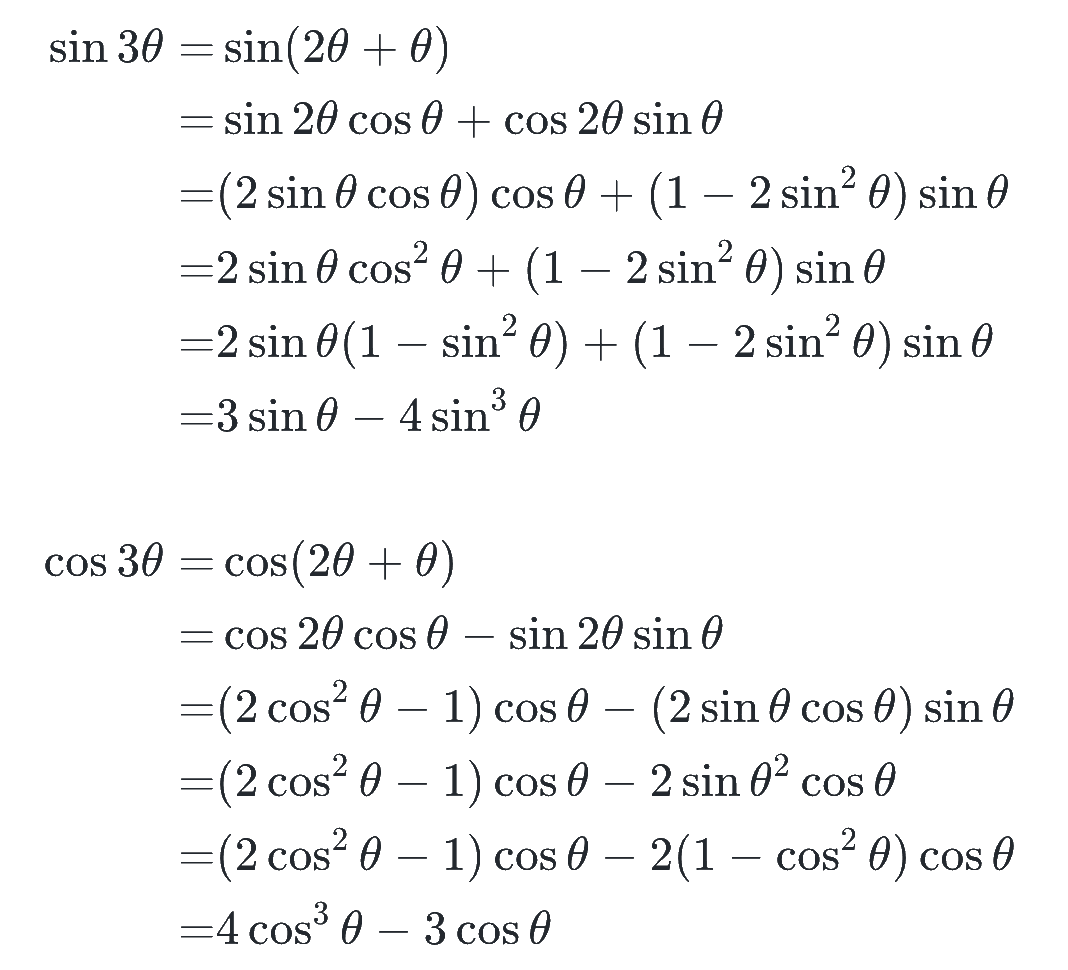
では、問題を解きながら、これらの倍角・半角の公式の知識を定着させましょう。（答えがすぐ下にあるので注意）

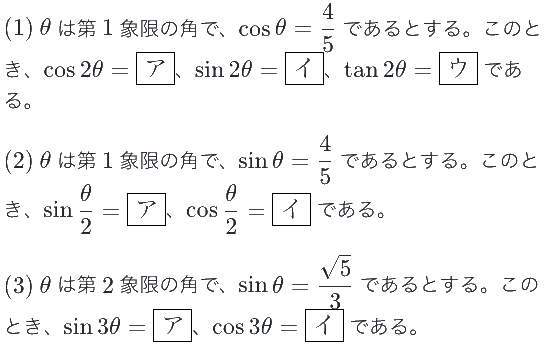
※弊社サービスのチェックテスト作成ツール「Dr.okke」より引用。1分で楽に、このようなチェックテストが作れます。

答：(1) 7/25・24/25・24/7 (2) √5/5・2√5/5 (3) 7√5/27・22/27

積和の公式

ここからはやや応用編です。もう一息です！

sin や cos 同士の積は、下の積和公式により和や差の形に変換できます。

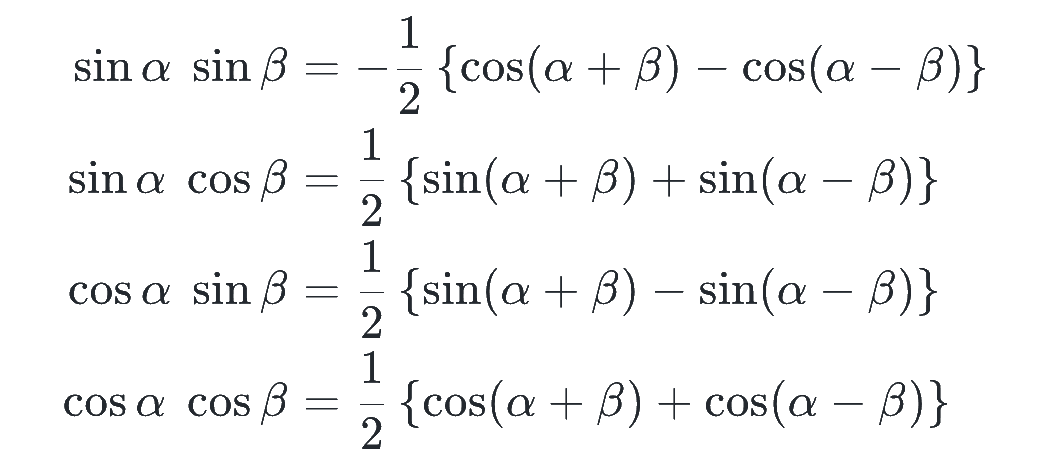
まずは、右辺を加法定理で展開すると左辺になることを各自確認してみましょう。

その上で、sin や cos 同士の積は和や差の形に変換できるということだけを覚えておいて、必要になったら思い出せばOKです。

思い出し方としては、たとえば sinα sinβ の形の場合を考えると、

• この形が出てくる加法定理（sin か cos か）を思い出す

  （例：sinα sinβ は cos の加法定理に登場する）

• cos(α+β) と cos(α-β) を組み合わせて、sinα sinβ だけの形にできないか考える

  （例：この場合は cos(α+β) - cos(α-β) と引き算すれば、余計な cosα cosβ の項が消える）

• 最後に、係数や符号を調整する

  （例：この場合は、cos(α+β) - cos(α-β) を計算すると -2sinα sinβ になるので、-1/2 を掛ければ、sinα sinβ になる。これで1つ目の積和公式を作れた！）

の流れで作れます。他の3つについても同様に作れるので、最初は大変でも自力で作れるようにしておきましょう。

和積の公式

sin や cos の和や差は、下の和積公式により積の形に変換できます。

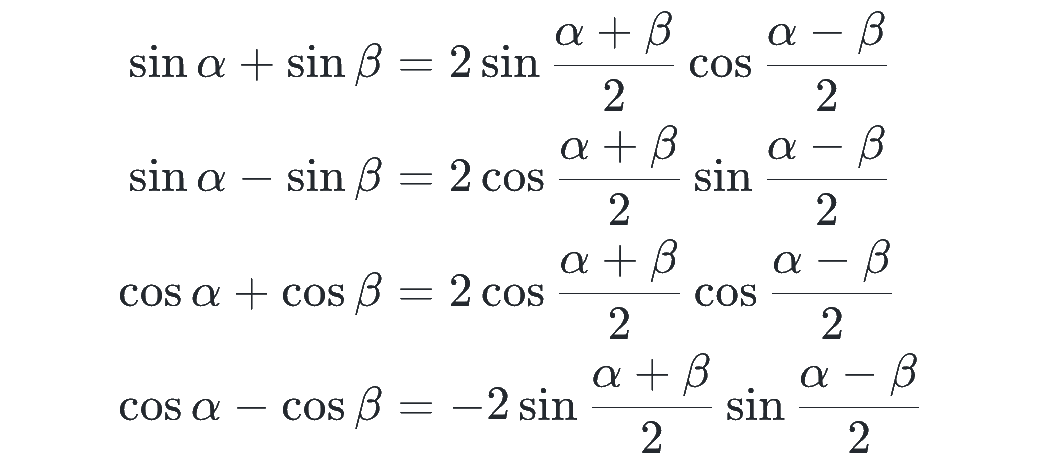
これについては、以下のように、α と β を同じ式の和と差で分解できることを知っておけば、全て加法定理から作ることができます。

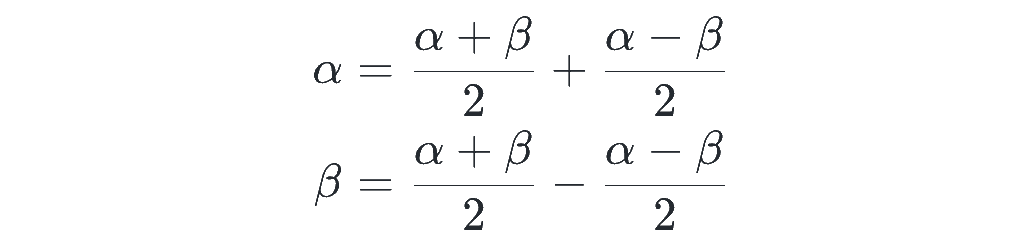
例えば一番上の和積公式については、α と β を上の式で分解して加法定理を使うと、

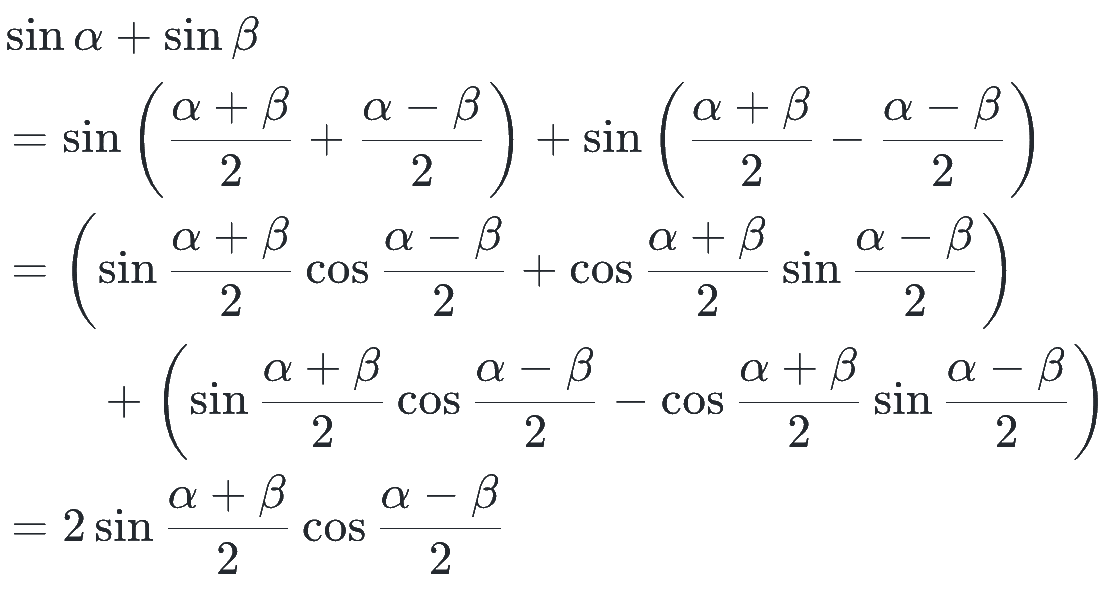
として作ることができます。

他の3つについても同様に作れるので、sin や cos の和や差は積の形に変換できるということと、上の α と β の分解式だけ覚えておいて、いつでも作れるようにしておきましょう！

積（掛け算）の形に変形できると、たとえば方程式がとても解きやすくなるので、使う場面も割と多い公式です。

また、この和積公式は、α と β という異なる角度の sin や cos の和と差に対して役に立つ公式です。角度が同じ sin と cos の和であれば、下で紹介する三角関数の合成で1つにまとめることができるので、区別しておきましょう！

三角関数の合成

では、最後に三角関数の合成について。角度の同じ三角関数の和

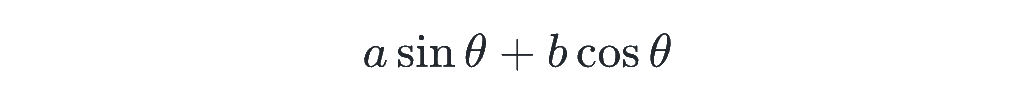
を、以下のように変形して、1つの形にまとめることを三角関数の合成と呼びます。（a や b は 0 ではないとします）

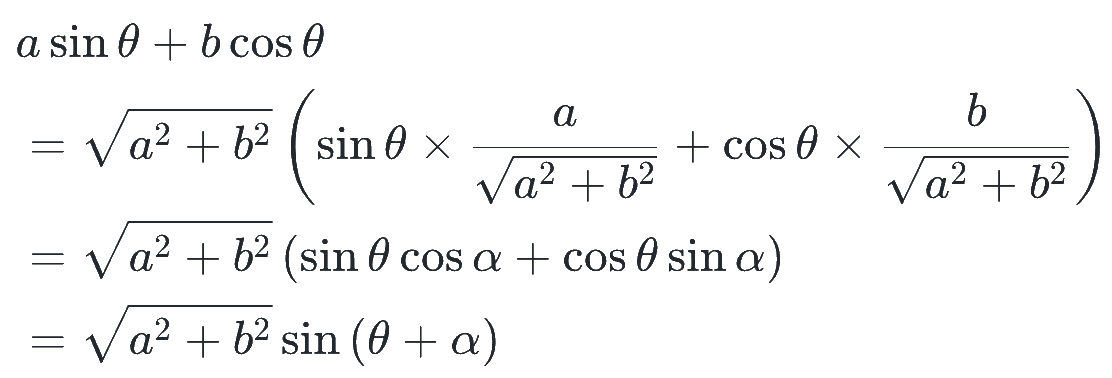
ただし、途中でいきなり現れた角度 α は、

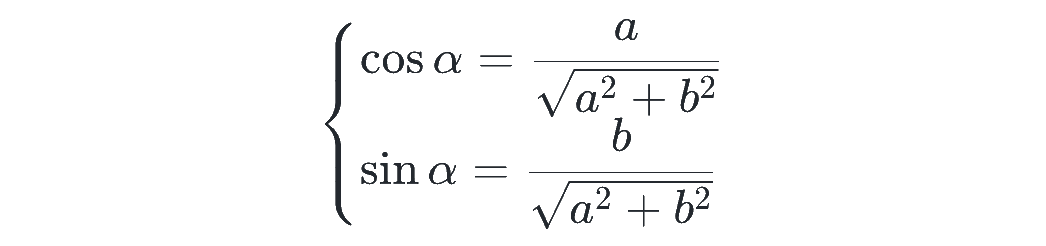
を満たす角で、このような α は 0≦α<2π で必ずただ1つに決まります。

係数の2乗の和で無理やりくくり出すことによって、うまく加法定理が使える形に変形できる、というのが合成のポイントです！覚えるようなものではないので、自力で変形できるようにしておきましょう。

α を図形的に示すと、以下の通りとなります。

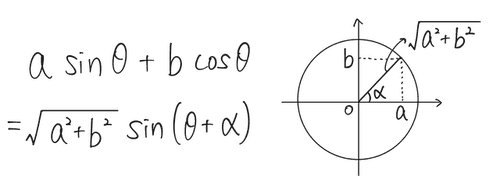
また、上では sin の加法定理を使って変形しましたが、同じように考えて、角度の取り方を変えて cos の加法定理を用いると、cos で合成することもできます。（cos の合成もときどき出てくるので知っておきましょう。やり方は全く同じです！）

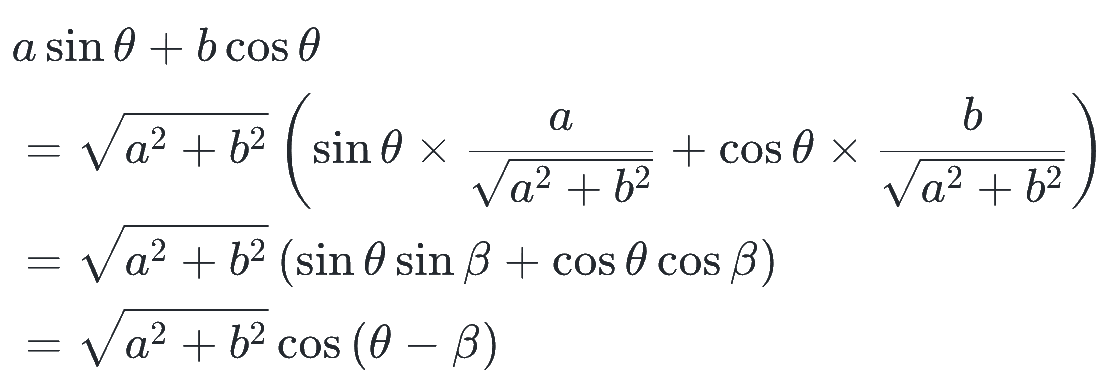
ただし、角度 β は、

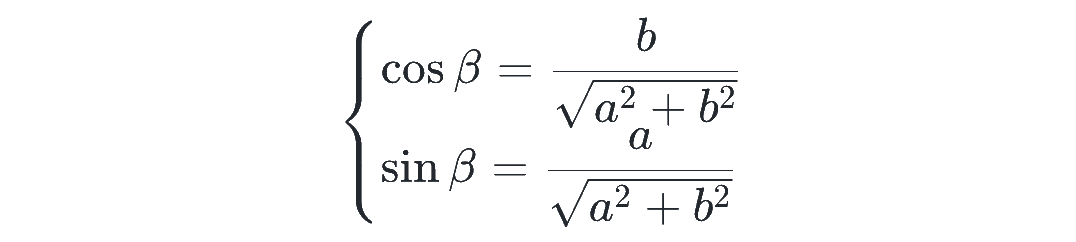
を満たす角で、このような β も 0≦β<2π で必ずただ1つに決まり、上の三角形を考えれば、β = π/2 - α が成り立つこともわかります。

では、問題を解きながら、これらの積和・和積公式と、三角関数の合成の知識を定着させましょう。（答えがすぐ下にあるので注意）

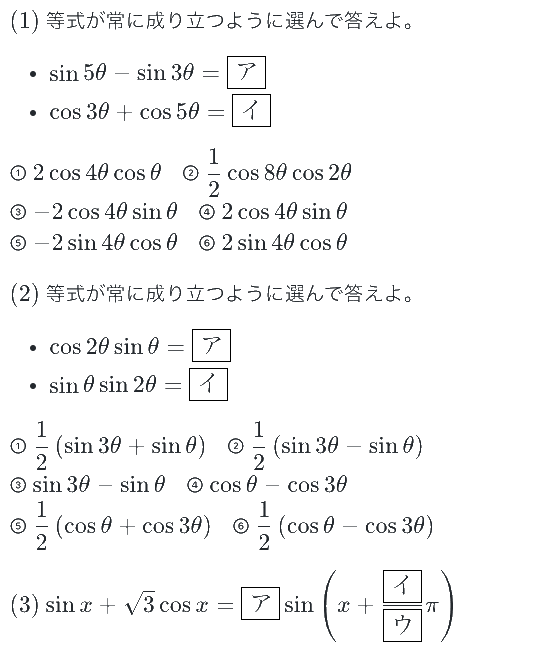
※弊社サービスのチェックテスト作成ツール「Dr.okke」より引用。1分で楽に、このようなチェックテストが作れます。

答：(1) 4・1 (2) 2・6 (3) 2・1・3

Dr.okkeの導入をご検討の方は、こちらの画像をタップし、無料トライアルをお試しください！

三角関数をマスターできる参考書を紹介！

三角関数の学習は大きく分けて、

• 公式を正しく使えるようにすること（毎回導出しながら、すぐにその場で思い出せるようにしていくことが大切）

• それぞれの公式を使う場面を見極めながら、本格的な問題を解けるようにすること

という2つのステップで進めていくのが良いでしょう。

特に1つ目の、公式をその場で思い出して、正しく使えるようにするためには、どうしても演習の量が大切になりますので、基本的には学校で配布される4STEPなどの傍用問題集や、チャート式などの網羅的な問題集といった、問題数の多い参考書に取り組むのがおすすめです。

その後、公式を使って本格的な問題を解いていく段階では、頭を整理しながら進めることも大事になりますので、解説が詳しい参考書を用いるのがオススメです。

ここでは、三角関数の演習量を確保しつつ、理解を深めるのにピッタリな参考書・問題集をいくつかご紹介しますので、参考書を買う際の参考になれば幸いです。

苦手な方向け

• 坂田アキラの三角関数が面白いほどわかる本 (坂田アキラの理系シリーズ)（坂田アキラ、KADOKAWA出版）

単元のピンポイントな学習に最適な、三角関数の範囲に特化した取り組みやすい参考書です。三角関数の基礎から丁寧に解説されているので、苦手な方や、学校の授業について行けなくなってしまって復習したい方に向いています。

• 数学Ⅱ・B 入門問題精講 改訂版（池田洋介、旺文社）

この参考書は、問題演習のみならず、各単元の導入から詳しく解説されているのが大きなおすすめポイントです。各単元の内容を理解した上で、取り組みやすい問題かつわかりやすい解説で知識を定着させていけるので、先取り学習や、弱点克服にとても役に立ちます。

数学2Bの他の単元も含まれますが、三角関数だけ取り組む、といったピンポイントな使い方もおすすめです。

公式を覚えて次のレベルに進みたい人向け

• 数学Ⅱ・B＋ベクトル 基礎問題精講（齋藤正樹・上園信武、旺文社） 

公式は覚えたし、教科書的な知識はあるのに、いざ模試などのテストになると三角関数が解けない方にとてもオススメの参考書です。厳選された良問を通じて、問題を解く上でのポイントを学べます。問題数もそこまで多くないので、三角関数だけ1週間でガッと強化する、といった使い方も可能です。

難関大レベルまで実力を伸ばしたい方向け

• 理系数学の良問プラチカ 数学ⅠAⅡBC (河合塾シリーズ 入試精選問題集 5)（大石隆司、河合出版） / 文系数学の良問プラチカ 数学ⅠAⅡBC(河合塾シリーズ 入試精選問題集 4)（鳥山昌純、河合出版）

応用レベルの頻出テーマが必要最小限の問題で網羅されており、解説も詳しいので、得点源にしたい場合には、これらの中の「三角関数」の範囲の問題を解いていくと効率が良いです。記述模試や実際の入試問題でよく見かけるテーマが凝縮されているので、模試や過去問になると解けなくなる方などにもおすすめです。

※「理系数学のプラチカ」よりも、「文系数学のプラチカ」の方が難しいので、注意してください。最難関大を目指す方以外は、文系の方であっても「理系数学の良問プラチカ」を使うのがおすすめです！

• ハイレベル数学Ⅰ・A・Ⅱ・B・C [ベクトル] の完全攻略 (駿台受験シリーズ)（米村　明芳・杉山　義明、駿台出版）

最難関大を目指す方にオススメな、いわゆる「ハイ完」です。問題数は少ないですが、とにかく解説が充実しており、初見の難問へ立ち向かう際の思考プロセスを身につけることができます。

演習量を増やし、知識を確実に定着させるならDr.okke

三角関数の分野では、公式の定着や、問題のパターンへの慣れがとても重要ですが、参考書では、すぐに下のポイントから公式が見えてしまったり、一度解いてしまうと「ここのページはこの解法だな…」と、問題の場所から公式や解法が推測できてしまったり、そもそも問題の解答を覚えてしまったりと、定着度の確認や効果的な反復演習を行うことが難しい場合も多いです。

そこで新しいテスト作成ツールであるDr.okkeをご紹介いたします。

いつでもすぐにテストを作成・実施

• 教科書の内容確認レベルの基礎から大学入試レベルの応用問題までを網羅しており、今日の授業でやったテーマに絞ったチェックテストから、分野を混ぜた実力テストまで、全て1分で簡単に作成可能です。

• 計算の一行問題に特化した「計算ドリル」という科目も別で用意しており、公式の運用や計算力をとにかく鍛えるといった使い方も可能です。

• 充実した良問とシャッフル出題によって、三角関数のそれぞれの公式や使い方を定着させられているかを確実にチェックできます。公式の数が多く、その定着が土台になる三角関数の力を引き上げるには、まさにピッタリのツールです。

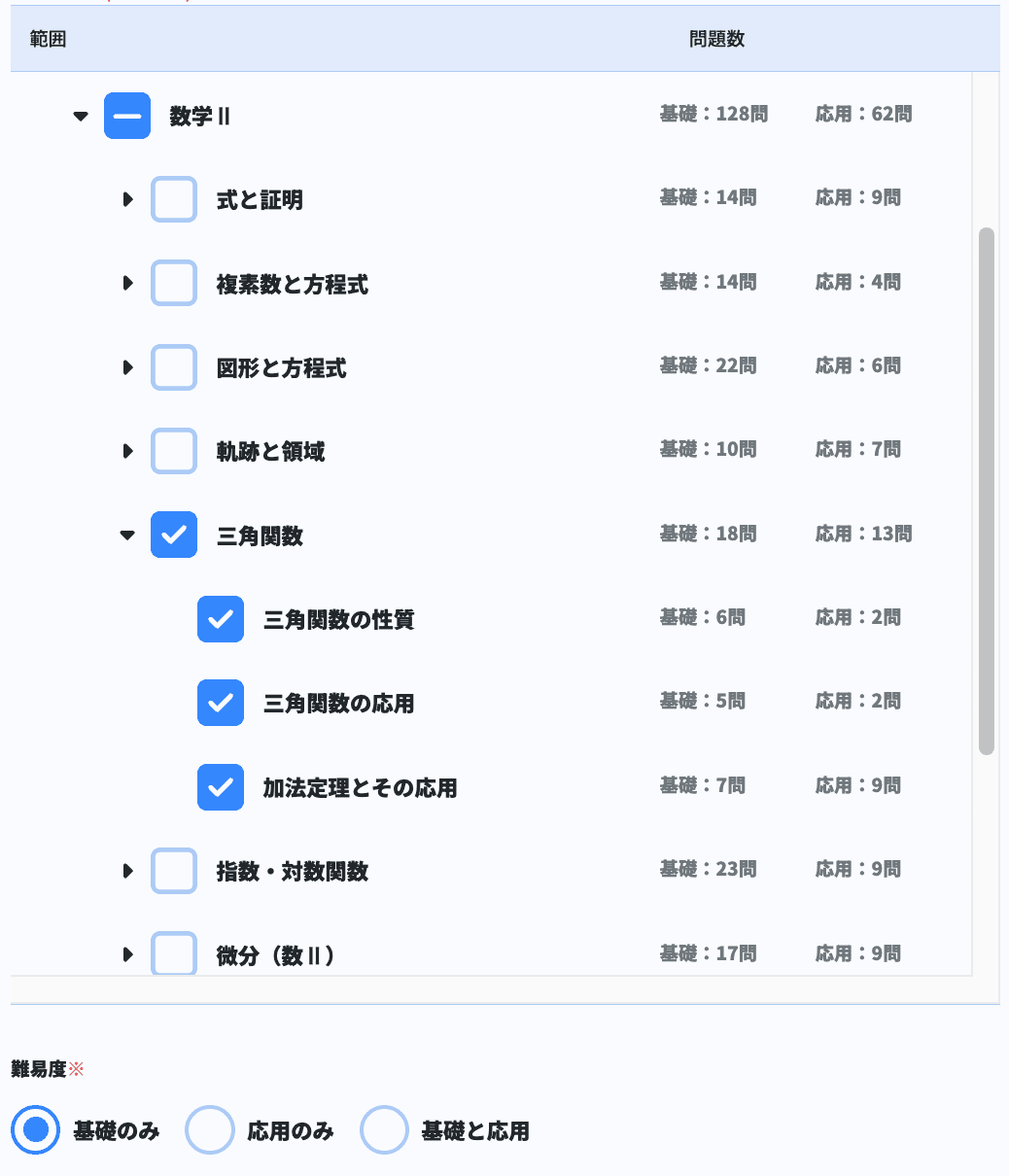
※ 難易度調整、制限時間設定も簡単にできます。

 自動採点かつ、受験結果のデータが蓄積

• テストを受けた直後に結果が表示され、解説も手作りでかなり詳しく作っているため、疑問を残さず、理解も深められます。

• 受験結果がデータとして自動で蓄積されるので、生徒さんの理解度や今復習すべき単元などが一目で分かります。これからのカリキュラムや学習計画を立てる際に、より一人ひとりに寄り添った指導を実現することができます。

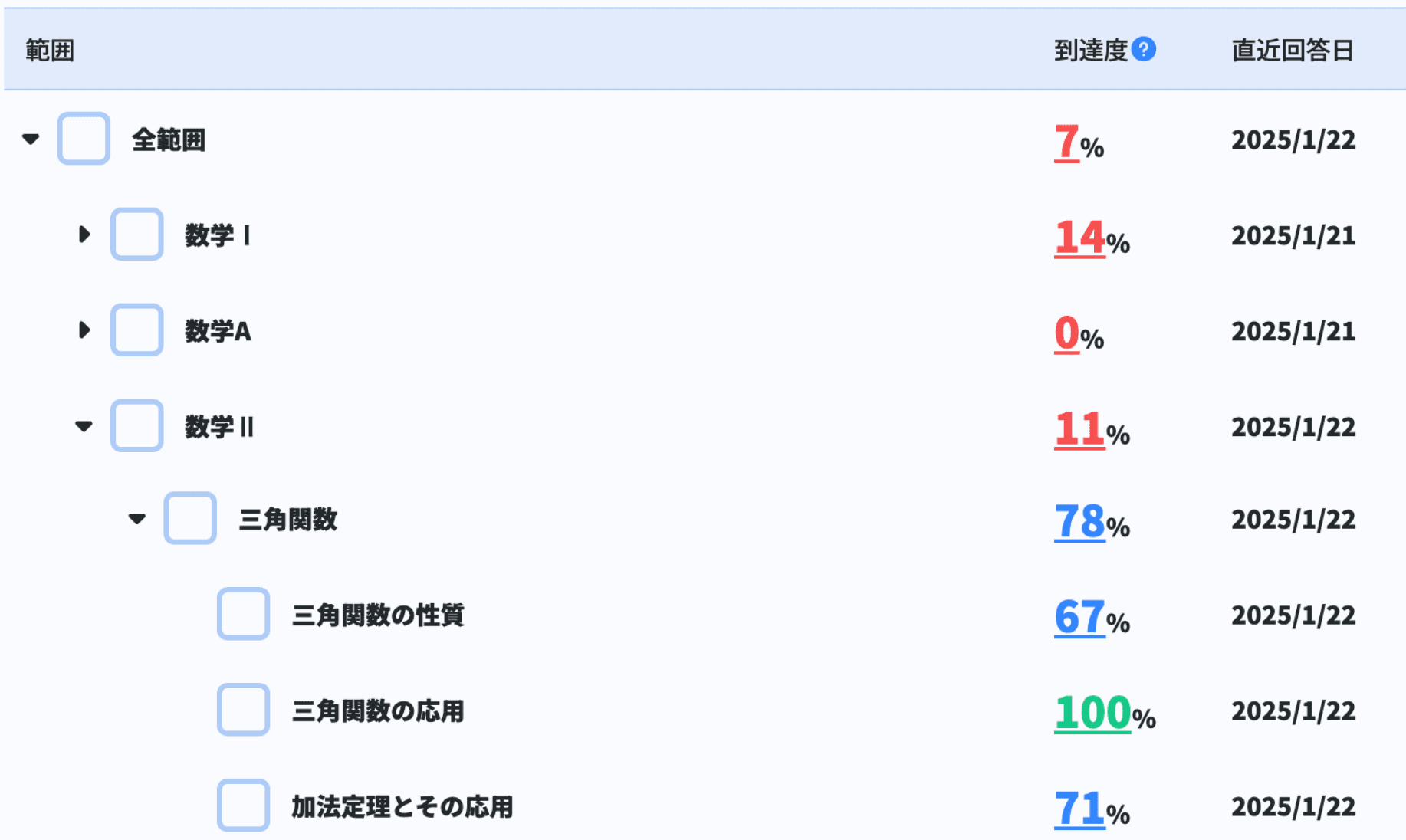
無料体験期間もありますので、ぜひ一度お試しください。

Dr.okkeの導入をご検討の方は、こちらの画像をタップし、無料トライアルをお試しください！わずか1分で確認テストの作成ができます！

まとめ

この記事では、三角関数の単元で出てくる公式を、導出や思い出し方を含めて総まとめするとともに、おすすめ参考書を紹介しました。公式がたくさん出てきますし、公式だけ覚えても、いざ問題を解こうとすると、どの式を使えば良いか戸惑ってしまうことが多く、苦手な方にとっては高い壁となりがちな単元です。

そこで学習の際にとても大切になるのは、公式を忘れてもすぐに思い出せるよう、普段の演習のときから「自力で作るクセ」をつけておくことと、自分の理解度に合った解説の詳しい参考書を選び、内容をしっかり理解した上で、その公式がどのような場合に使えるのかを合わせて押さえていくことです。毎回教科書の公式を見ながら問題を解いていては、いつまで経っても公式を思い出すことはできません。

また、使う式がわかって式が立てられても、計算が重たいことも多く、普段の演習から最後まで自分の手で計算するようにすることが重要です。

上で紹介したように、解説の詳しい市販の参考書や問題集もたくさんありますが、問題の並びで使う公式や解法が推測できてしまったり、最後まで解き切らず、解法だけ合っていたら先に進んでしまったりと、どうしても効果的な学習ができないこともあります。その際には、Dr.okkeのようなテストツールを有効活用し、定着させられているかを確認しながら着実に学習を進めていくことが、三角関数の得点アップへの近道となるでしょう。（もしDr.okkeにご興味がありましたら、こちらまでご連絡ください。無料トライアル実施中です！）

三角関数は手強い単元ですが、模試や受験ではとにかくよく出てきますし、慣れてしまえば得点源にできます。ぜひこの記事を参考に克服し、試験本番で確実に解けるように効果的に学習に励んでいきましょう。