はじめに

「ベクトル」は2025年度入試以降、新しい学習指導要領のもとで数学Bから数学Cに移行しますが、文系であっても大学受験では数学ⅠAⅡBC（実質ベクトルのみ）までは基本的に出題されることになり、依然重要な単元となっています。

※参考：新課程の大学入試出題範囲について

各大学の対応はこちらを参照してください。

ベクトルは高校に入ってから新しく導入される概念で、一度苦手だと感じてしまった生徒さんはなかなかその感覚から抜け出せなくなることが多いのではないでしょうか。例えば、頻出テーマである、分点の位置ベクトルや内積、同一直線上・同一平面上にある条件、ベクトル方程式は、理解できるまでに時間がかかることが多く、ベクトルをわからないと感じさせる大きな要因となっています。

また、公式を覚えても問題でいざ式を立てようとするとうまく式が組み立てられず、その先に全く進めないというケースも十分あり得るでしょう。

※参考：ベクトルが苦手な人必見！ベクトルが難しい理由と攻略する方法｜横浜の個別塾

本記事では「ベクトル」の何が難しいのかを解説したうえで、オススメの考え方、ベクトルを攻略するためにおすすめの参考書について解説していきます。ぜひ最後まで読んでみてください。

💡ベクトルの強化・定着チェックならDr.okke💡

数学Cに移っても、依然として頻出単元である「ベクトル」。
しかし、指導現場では以下のような悩みも多いのではないでしょうか。

• 図もあるので、自力で問題を作るのは大変で、生徒がどこまで定着できているかのチェックが難しい...

• 参考書や問題集だと問題数が多く、短期間での弱点克服には使いづらい...

• 生徒ごとの実力差が大きいが、個別対応をする時間が無い...

こうした悩みを解決できるのが、学習ツール 「Dr.okke（ドクターオッケ）」 です。
Dr.okke なら、

• 各生徒の弱点に応じて、個別最適なテストを1分で作成でき、客観的な定着度がすぐにわかる

• 選び抜かれたオリジナルの良問を通じて、ベクトルの基礎から応用まで短時間で強化できる

• 手作りの詳しい解説や関連動画で、確実に理解できる

先生方の指導を効率化しつつ、生徒の成績アップをしっかりサポートします。

👉無料トライアルでさっそくテストを作成する

ベクトルは何が難しいのか？

ベクトルはこれまで習ってきたものとは概念が異なります。特に多くの人を悩ませるのは、「大きさ」と「方向」の両方の性質を併せ持つという点でしょう。「要するに矢印だ」、と教わることも多いと思いますが、最初に聞いても意味がわからないと思います。

また、そういったベクトルの性質から、ベクトルのまま表記して解いていく場合と、成分で表記して解いていく場合が出てくるので、問題によって何をすれば良いかが分かりづらいことが多いです。その結果、先ほども述べた通り、公式を覚えたとしても、問題に応じてどの公式を使えばいいかわからないことになりがちです。

そのため、学ぶ際には単に公式の形のみを覚えるのではなく、その公式がどのような場合に使えるのかを合わせて押さえていくのがコツです。

例えば、内積の求め方は大きく分けて2つありますが、ベクトルの大きさやなす角が分かっている場合に用いる式と、それぞれの成分がわかっている場合に用いる式があり、使い方が異なります。

※参考：内積の求め方｜okke 用語

このようにとっつきにくいベクトルですが、ややこしい性質を持つ分、ベクトルをうまく用いると図形問題がすっきり解けることも多いです。受験でも、一見するとベクトルの問題でなくても、ベクトルの考え方を使うことで楽に解ける図形問題も多く、道具として自在に使いこなせるようになるまで我慢強く学んでいくことが大切です。それを積み重ねることで、初めわけがわからなかったベクトルの概念についても、少しずつ感覚が掴めてくるはずです。

以下、すでに基礎事項を学び終えている方向けになりますが、ベクトルと図形問題のつながりについて、具体的に2つ紹介します。

①内積とは何か？

上でも述べた内積については、実は面白い図形的性質があります。

参考：内積の図形的意味｜okke 用語

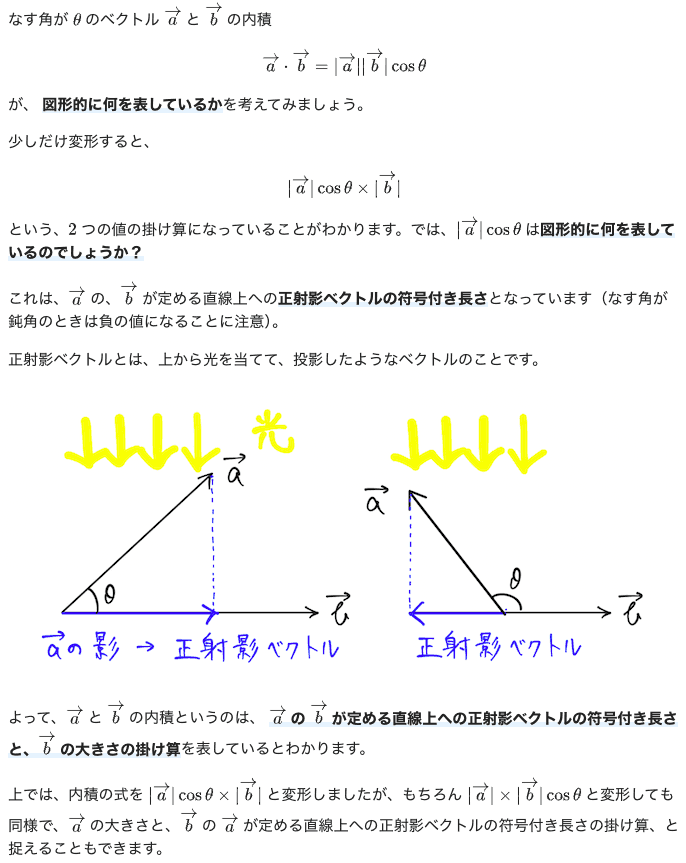
このイメージを頭に入れておくと、内積の問題でも図形的な発想ですぐに解けてしまうこともあるので、とてもオススメです。

②幾何とベクトルが組み合わさる頻出問題

ベクトルを活用すると、同一直線上・同一平面上にある条件などを立式しやすくなり、例えば線分の比といった図形量を求めやすくなることも多いです。

このパターンの問題は、平面・空間を問わずとても頻出なので、与えられた条件をベクトルで表していき、数式に落とし込んで素早く解いていく流れを、しっかり身につけておきましょう。計算が重たくなることも多いです。

例えば以下のような空間ベクトルの【例題】で考えてみましょう。

※出典：Dr.okke

この【例題】では座標が記載されていませんし、パッと見てベクトルも登場しませんが、重心や内分点の比について言及されていることからベクトルで考えるのが有効です。

点Eがどのような点か、それをベクトルで表すには何を用いたらいいかを考えることで、自然と立てるべき条件が分かります。この発想はとても大事で、この考え方ができると公式の使い方で迷わなくなります。

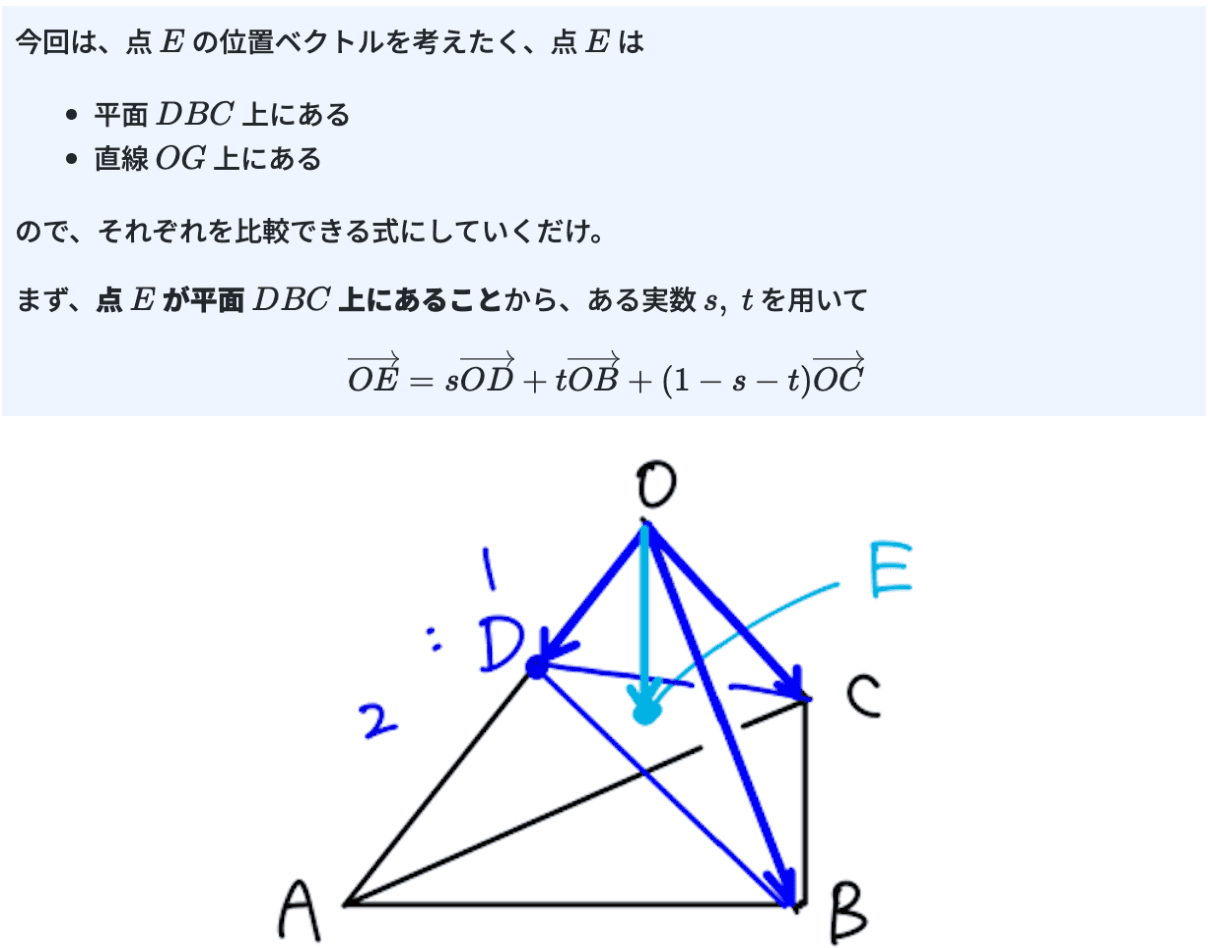
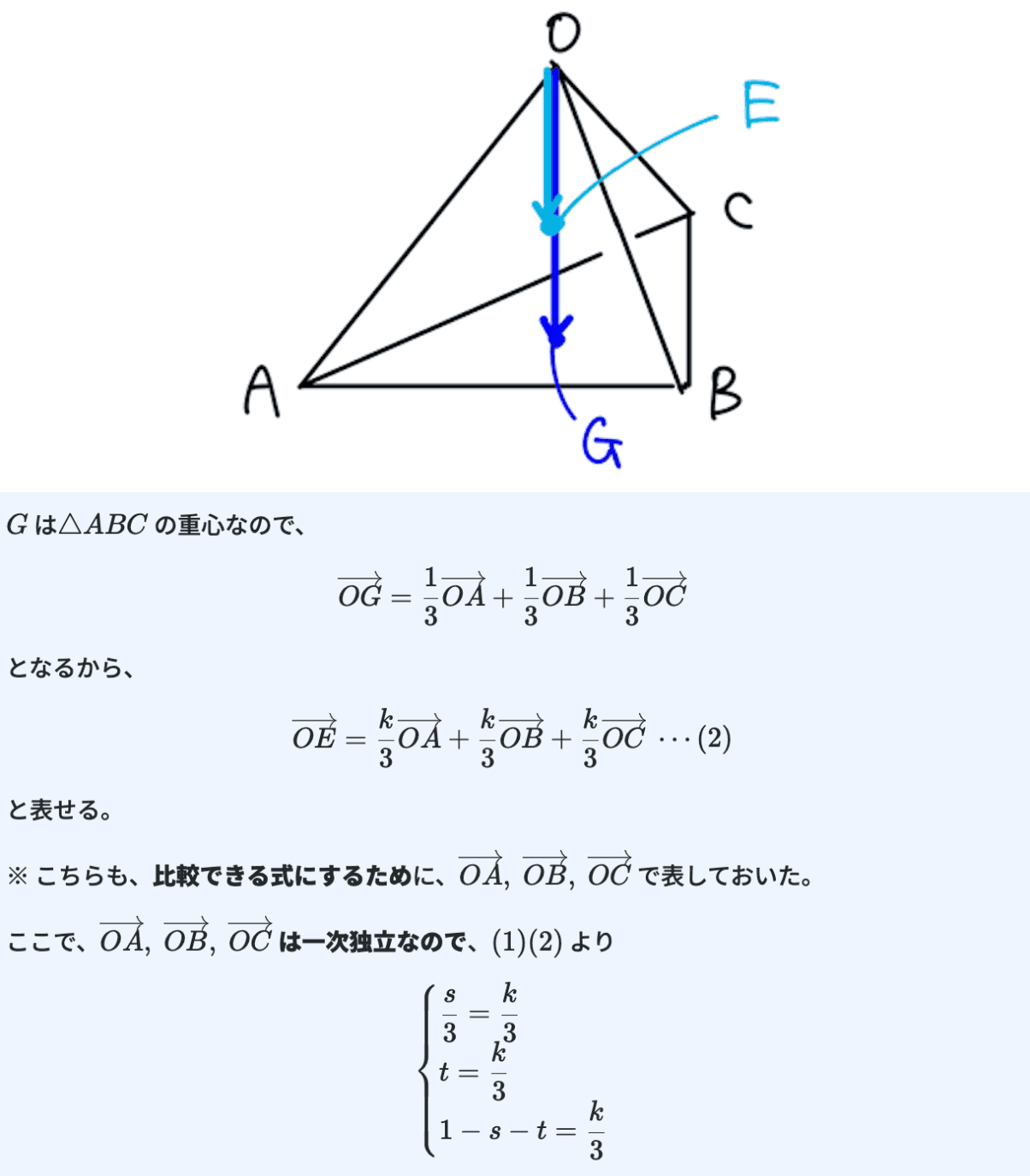
※出典：Dr.okke

このように、与えられた条件をベクトルで表していき、数式に落とし込んで解いていく流れは本当にワンパターンなので、確実にできるようにしておきましょう。

ベクトルで表すときに、何の公式を使ったらいいか初めは迷うと思います。繰り返しになりますが、上の例題の最初に点Eがどんな点かを考えたように、考えている点がどのような点なのか、それをベクトルで表すには何を用いたらいいかを考えれば、自然と立てるべき条件が定まります。

💡ベクトルの強化・定着チェックならDr.okke💡

数学Cに移っても、依然として頻出単元である「ベクトル」。
しかし、指導現場では以下のような悩みも多いのではないでしょうか。

• 図もあるので、自力で問題を作るのは大変で、生徒がどこまで定着できているかのチェックが難しい...

• 参考書や問題集だと問題数が多く、短期間での弱点克服には使いづらい...

• 生徒ごとの実力差が大きいが、個別対応をする時間が無い...

こうした悩みを解決できるのが、学習ツール 「Dr.okke（ドクターオッケ）」 です。
Dr.okke なら、

• 各生徒の弱点に応じて、個別最適なテストを1分で作成でき、客観的な定着度がすぐにわかる

• 選び抜かれたオリジナルの良問を通じて、ベクトルの基礎から応用まで短時間で強化できる

• 手作りの詳しい解説や関連動画で、確実に理解できる

先生方の指導を効率化しつつ、生徒の成績アップをしっかりサポートします。

👉無料トライアルでさっそくテストを作成する

ベクトルのおすすめの参考書

ベクトルはこのように、その場でどう式を組み立てるかが勝負の分かれ目になるので、一つ一つの公式の内容の暗記よりも、公式をどう使うか、演習を通じて慣れていくことが重要です。

演習の際には、基本的には学校で配布される問題集などを用いても良いですが、ベクトルの問題では計算が複雑になることも多く、解説が詳しい参考書を用いるのがオススメです。ここではベクトルの理解を深め、演習量を確保するのにピッタリな参考書・問題集をいくつかご紹介しますので、参考書を買う際の参考になれば幸いです。

まず、単元のピンポイントな弱点克服に最適な、ベクトルに特化した参考書・問題集を紹介します。

苦手な方向け

• 坂田アキラのベクトルが面白いほどわかる本 (坂田アキラの理系シリーズ)

• 細野真宏のベクトル [平面図形] が本当によくわかる本 /  細野真宏のベクトル [空間図形] が本当によくわかる本

• 坂田アキラのベクトルが面白いほどわかる本 (坂田アキラの理系シリーズ)（坂田アキラ、KADOKAWA出版）

ベクトルの基礎から丁寧に解説されているので、苦手な方や、学校の授業について行けなくなってしまって復習したい方に向いています。

• 細野真宏のベクトル [平面図形] が本当によくわかる本 /  細野真宏のベクトル [空間図形] が本当によくわかる本（ともに細野真宏、小学館）

こちらもベクトルに特化して、基礎から丁寧に解説された参考書で、ベクトルの平面図形と、空間図形についてのバージョンがそれぞれ出版されています。解説が詳しいです。

公式は覚えたから次のレベルに進みたい人向け

• ベクトルの集中講義 (教科書Next)（東京出版編集部）

教科書的な知識はあるのに、いざ模試や過去問になるとベクトルが解けない方にとてもオススメの参考書です。テーマごとに、解説＋問題演習という構成になっており、深く理解することができます。

難関大レベルまで実力を伸ばしたい方向け

• 数学 ベクトル 分野別標準問題精講

• 文系数学の良問プラチカ 数学ⅠAⅡB (河合塾シリーズ 入試精選問題集 4)

• 理系数学の良問プラチカ 数学ⅠAⅡB (河合塾シリーズ 入試精選問題集 5)

• 数学 ベクトル 分野別標準問題精講（永曽仙夫、旺文社）

問題数は45題と、とても多いわけではないですが、難易度の幅が設けられており、入試標準レベルから難関レベルの良問が収録されているので、ベクトルについて一気に実力を固めることができます。

以下は、他の分野も含んでいるものの、ベクトルだけ解くことで実力を強化できる問題集になります。

・文系数学の良問プラチカ 数学ⅠAⅡB (河合塾シリーズ 入試精選問題集 4)（鳥山昌純、河合出版）/ 理系数学の良問プラチカ 数学ⅠAⅡB (河合塾シリーズ 入試精選問題集 5)（大石隆司、河合出版）

応用レベルの頻出テーマが必要最小限の問題で網羅されており、解説も詳しいので、ベクトルを得点源にしたい場合には、これらの中の「ベクトル」の問題を解いていくと効率が良いです。記述模試や実際の入試問題でよく見かけるテーマが凝縮されているので、模試や過去問になると解けなくなる方などにもおすすめです。

※「理系数学の良問プラチカ 数学ⅠAⅡB」よりも、「文系数学の良問プラチカ 数学ⅠAⅡB」の方が難しいので、注意してください。最難関大を目指す方以外は、文系の方であっても「理系数学の良問プラチカ」を使うのがおすすめです。

• ハイレベル数学Ⅰ・A・Ⅱ・B・C [ベクトル] の完全攻略 (駿台受験シリーズ)（米村　明芳・杉山　義明、駿台出版）

最難関大を目指す方にオススメな、いわゆる「ハイ完」です。問題数は少ないですが、とにかく解説が充実しており、初見の問題への対応力も鍛えられます。

演習量を増やすならDr.okke

初見の問題への適応力が要求されるベクトルですが、一度参考書を解いてしまうと「ここのページはこの解法やその類似パターンだな…」と、問題の場所から公式や解法が推測できてしまったり、そもそも問題の解答を覚えてしまったりと、効果的な演習を行うことが難しい場合も多いです。

そこで新しいテスト作成ツールであるDr.okkeをご紹介いたします。

いつでもすぐにテストを作成・実施

- 教科書の内容確認レベルの基礎から大学入試レベルの応用問題までを網羅しており、全体の完成度を測るテストから今日の授業でやった単元に絞った確認テストまで、全て1分で簡単に作成可能です。

ベクトルであれば、平面ベクトルと空間ベクトル、演算と図形との融合問題にそれぞれ分けてテストを実施できます。

- 充実した良問とシャッフル出題によって、ベクトルの公式や使い方を定着させられているかを確かめられます。暗記で対応できないベクトルの実力を確認・養成するには、ピッタリのツールです。

難易度調整、制限時間設定も簡単にできます。

 自動採点かつ、受験結果のデータが蓄積

- テストを受けた直後に結果が表示され、解説も充実しているため、ただ問題を解くよりも理解を深められます。本記事で扱った例題とその解説もDr.okke内に収録されているものです。

- 受験結果がデータとして自動で蓄積されるので、生徒さんの理解度や今復習すべき単元などが一目で分かります。これからのカリキュラムや学習計画を立てる際に、より一人ひとりに寄り添った指導を実現することができます。

無料体験期間もありますので、ぜひ一度お試しください。

まとめ

ベクトルは突如出てくる新しい概念であり、公式の形だけ覚えても、いざ問題演習をしようとすると、どのように式を立てればよいのか戸惑ってしまうことが多く、苦手な方にとっては高い壁となりがちです。

そこで大切なのは、自分の理解度に合った解説の詳しい参考書を選び、内容をしっかり理解した上で、様々なパターンの問題に数多く取り組みながら、公式の形のみではなくその公式がどのような場合に使えるのかを合わせて押さえていくことです。

また、使う式がわかって式が立てられても、計算が重たいことも多く、普段の演習から最後まで自分の手で計算するクセをつけることが重要です。

上で紹介したように、解説の詳しい市販の参考書や問題集もたくさんありますが、問題の並びで使う公式や解法が推測できてしまったり、最後まで解き切らず、解法だけ合っていたら先に進んでしまったりと、どうしても効果的な学習ができないこともあります。その際には、Dr.okkeのようなテストツールを有効活用し、定着させられているかを確認しながら着実に学習を進めていくことが、ベクトルの得点アップへの近道となるでしょう。（もしDr.okkeにご興味がありましたら、こちらまでご連絡ください。）

ベクトルは手強い単元ですが、模試や受験では頻出です。ぜひこの記事を参考に克服し、入試本番で高得点を取れるよう学習に励んでいきましょう。